目录

• 1. 朴素的模式匹配
• 2. KMP算法解决的问题
• 3. KMP算法
• • 公共前后缀（重点）
  • next 数组
  • KMP算法实现

1. 朴素的模式匹配

• 朴素算法中，当匹配到不同位时，主串指针i会退回到该次匹配起点处的下一位置，以其为下一次匹配的主串起点

• 同时字串的j指针退回其起始位置

• 如此一来每次匹配主串指针后移一位，字串指针始终在其起始位置

• 时间复杂度为O(m*n)

2. KMP算法解决的问题

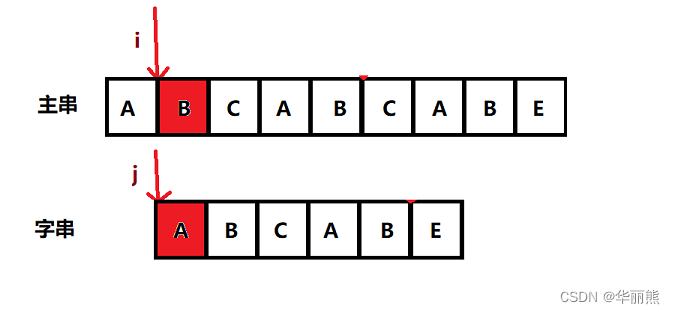
• 可以发现下图中，在第二次匹配时，第一个元素就已经不一样了

• 朴素算法的缺点就在于其会傻傻的执行许多次这样不必要的判断

• 这就是KMP算法所解决的问题

3. KMP算法

• 主串指针不会进行回溯，不会回到朴素匹配中的下一匹配点
• 利用已匹配部分中的公共前后缀来调整字串指针位置，以此加速下一次匹配

根据下面的动画感受感受

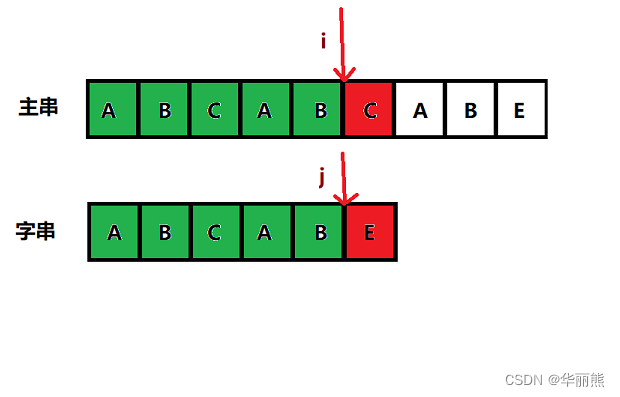
• 可以看到，主串指针( i )在整个查找过程中都没有前移，每次查找的起点均为上次查找的结束点，即 i 永远不递减，这也使KMP的精髓
• 同时，当不匹配位置前一位对应的next数组中元素不为0时，字串指针( j )会向后偏移相应个数的字符
• 这样一来，无论是主串还是字串的判断次数都得到了优化，时间复杂度优化至O(m+n)

公共前后缀（重点）

公共前后缀的计算：
这里用公式理解，计算下标为a处的公共前后缀个数，如果[a-x,a]范围的每一个元素与[0,x]范围的每一个元素相等，则a处的公共前后缀个数为x+1

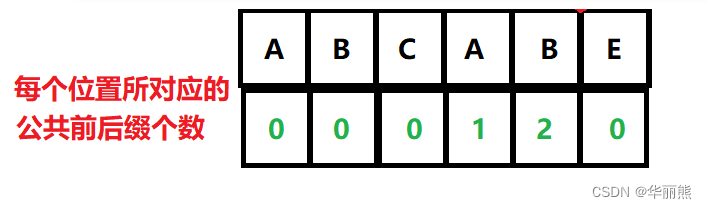
这里注意找某一位置的公共前后缀时，要将起始位置的字符同该位置字符比较，而不是只要在该位置之前出现了相同元素就判断存在公共前后缀
如下图中的红色位置B，虽然在其之前存在一个字符B，但是该位置的公共前后缀为0

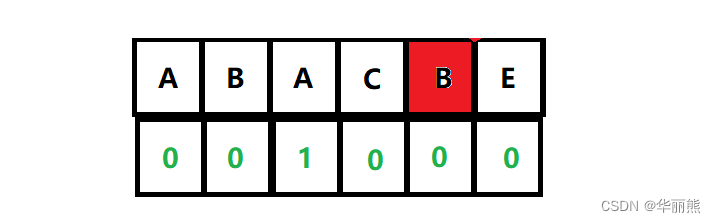
next 数组

理解了什么是公共前后缀，其实next数组就是存储该数组每个对应位置公共前后缀数量的数组
代码实现next数组

int* get_next(const char* p)
{assert(p);int len = strlen(p);int* next = (int*)malloc(sizeof(int) * len);if (next == NULL){return NULL;}else{//先将其全部初始化为0memset(next, 0, sizeof(int) * len);int j = 0;int i = 0;for (i = 1; i < 6; i++){if (p[i] == p[j]){next[i] = next[i - 1] + 1;j++;}else{j = 0;}}return next;}
}

KMP算法实现

注意代码注释

int my_kmp(char* a1, char* a2)
{int* next = get_next(a2);int len1 = strlen(a1);int len2 = strlen(a2);int i = 0;int j = 0;while (i < len1){if (a1[i] == a2[j]){i++;j++;}else if (j > 0)  // j>0 时，根据next数组调整 j 的位置j = next[j - 1];else   //字串第一个字符就不匹配i++;if (j == len2) //匹配成功，返回值为字串第一个字符在主串中的位置return i - j;}return -1;
}