二叉链表、三叉链表定义：

#include
using namespace std;typedef int Status;
#define MAXTSIZE 100typedef char TElemtype;//根据需求情况修改
typedef TElemtype SqBiTree;//sequence binary tree
//binary：二进制的; 二元的; 由两部分组成的;
SqBiTree bt;//binary treestruct BiNode//二叉链表存储结构
{TElemtype data;structBiNode* lchild, * rchild;//左右孩子指针
};
typedef BiNode * BiTree;struct TriNode//trinary：三元的
{TElemtype data;structBiNode* lchild, * rchild,* parent;
};
typedef TriNode* TriTree;int main()
{}

遍历二叉树具体实操：

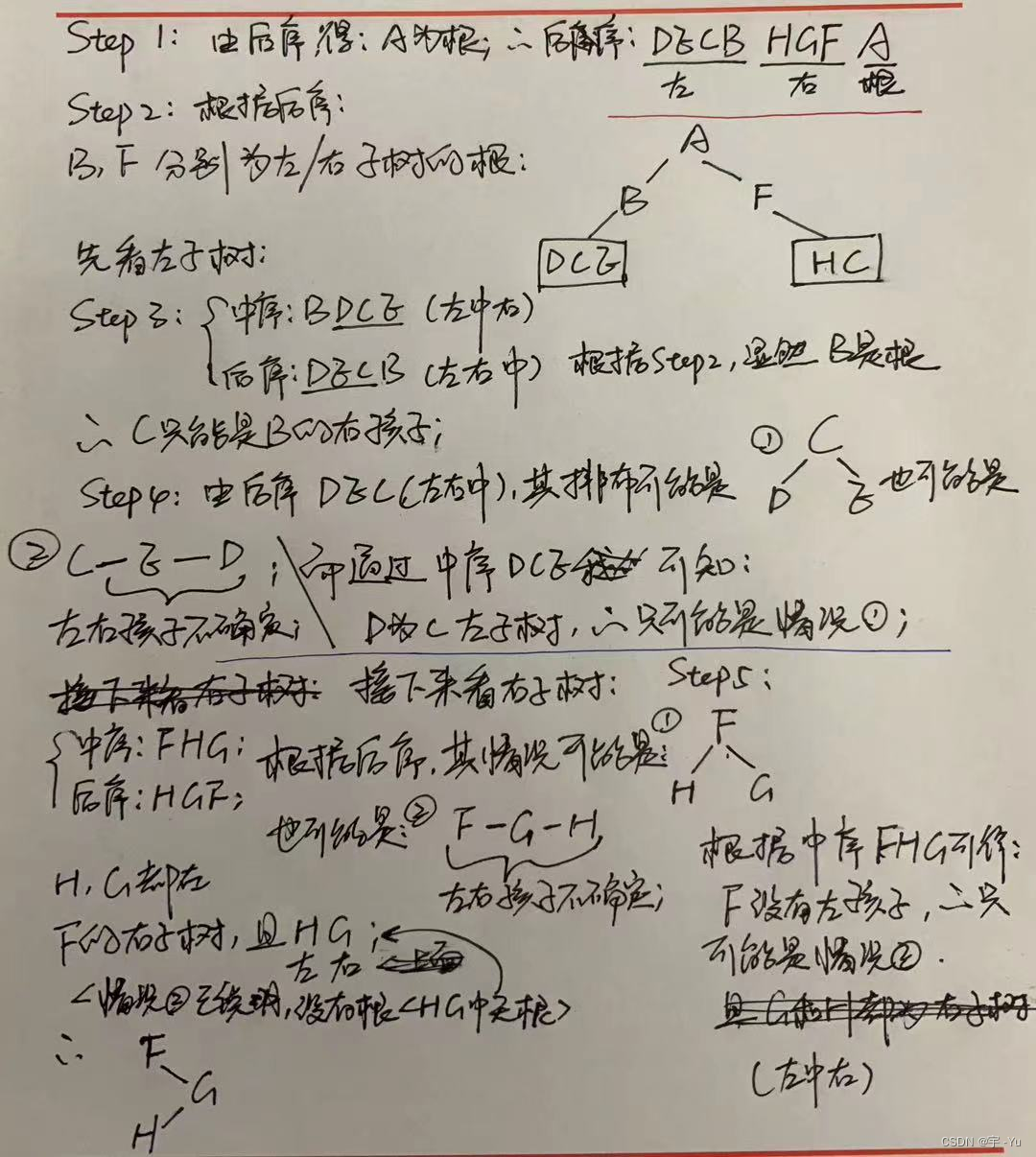
最终结果：

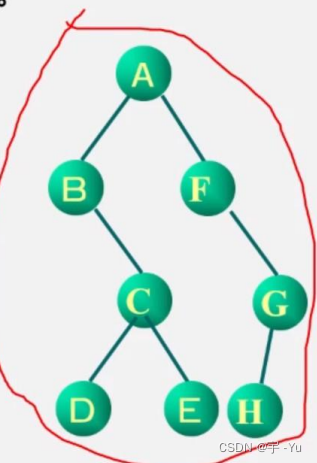
遍历的实现：

递归遍历程序实现：

三种遍历算法的代码模块

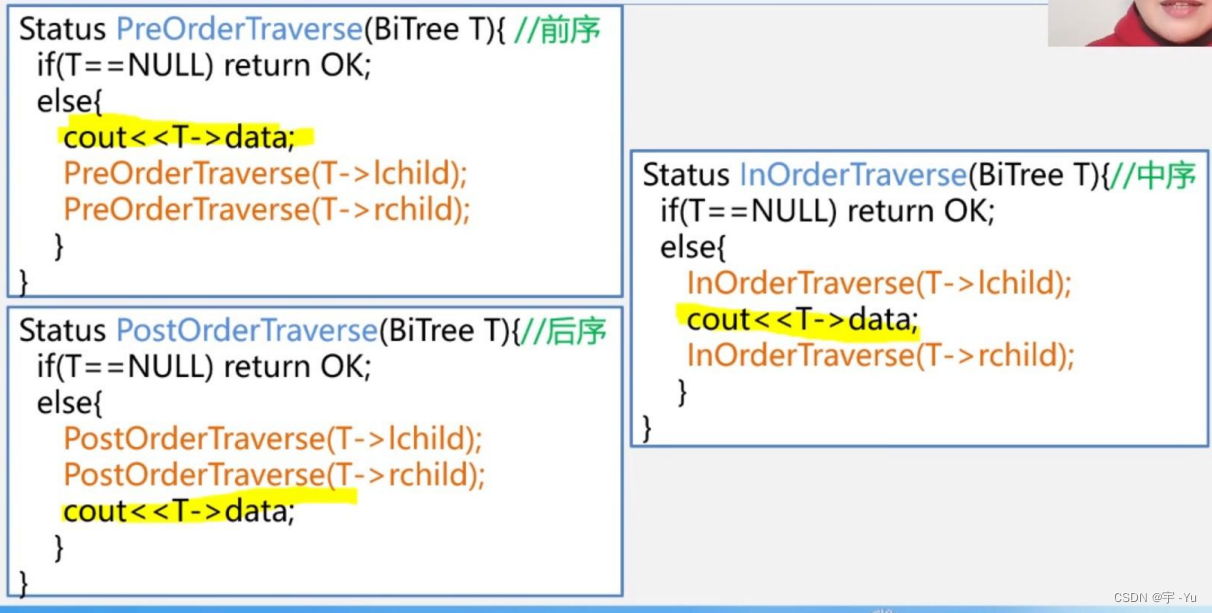
为了文档的简洁性，避免赘述，我们这里只写先序遍历的算法：（中序后序调换语句顺序即可）

void Pre(BiTree& T)
{if (T != NULL) {cout << T->data;//printf("%d\t{,T->data);Pre(T->lchild);Pre(T->rchild);}
}//注意Pre函数必须要写在遍历函数前面Status PreOrderTraverse(BiTree T)
{if (T == NULL)return 0;//空二叉树else{Pre(T);//visit(T);//访问根结点PreOrderTraverse(T->lchild);//递归遍历左子树PreOrderTraverse(T->rchild); //递归遍历右子树}
}

注：

//PPT上写的是
//void Pre(BiTree* T)
//但是我们的BiTree已经是一个指针类型，所以没必要再画蛇添足

这里：
void Pre(BiTree& T)

void Pre(BiTree T)

都可以

非递归遍历程序算法实现：

前置条件（二叉树和顺序栈的）：

//顺序栈
#include
using namespace std;
#include//存放exit
#include//OVERFLOW,exit#define TRUE        1
#define FALSE       0
#define OK          1
#define ERROR       0
#define INFEASIBLE  -1
//#define OVERFLOW   -2   #define MAXlength 100  
//可按需修改，PPT中写的是MAXlengthtypedef int Status;
typedef char  SElemType; 
typedef char TElemtype;//根据需求情况修改struct SqStack
{SElemType* base; //栈底指针  SElemType* top;//栈顶指针int stacksize; //栈可用最大容量
};//二叉树
#define MAXTSIZE 100typedef TElemtype SqBiTree;//sequence binary tree
//binary：二进制的; 二元的; 由两部分组成的;
SqBiTree bt;//binary treestruct BiNode//二叉链表存储结构
{TElemtype data;structBiNode* lchild, * rchild;//左右孩子指针
};
typedef BiNode* BiTree;//函数
Status InitStack(SqStack& S)//构造一个空栈
{S.base = new SElemType[MAXlength];//或//S.base = (SElemType*)malloc(MAXlength * sizeof(SElemType));if (!S.base) exit(OVERFLOW);// 存储分配失败S.top = S.base;//栈顶指针等于栈底指针S.stacksize = MAXlength;return true;
}Status StackEmpty(SqStack S)
{// 若栈为空，返回TRUE；否则返回FALSE if (S.top == S.base)return TRUE;elsereturn FALSE;
}int StackLength(SqStack S)
{return S.top - S.base;
}Status ClearStack(SqStack S)//清空顺序栈
{if (S.base)S.top = S.base;return OK;
}Status DestroyStack(SqStack& S)//销毁
{if (S.base){delete S.base;S.stacksize = 0;S.base = S.top = NULL;}return OK;
}Status Push(SqStack& S, SElemType e)
{if (S.top - S.base == S.stacksize)//不是MAXlengthreturn OVERFLOW;*S.top = e;S.top++;//也可以写成：//*S.top++ = e;return true;
}Status Pop(SqStack& S, SElemType& e)
//若栈不空，则删除S的栈顶元素，用e返回其值，并返回OK;	否则返回ERROR
{if (S.top == S.base) // 等价于 if(StackEmpty(S))return UNDERFLOW;//ERROR;e = *S.top;S.top--;//e = *--S.top;return true;
}

递归遍历程序算法实现：

以中序遍历为例：

思路：

有（根）结点：

1. 把根结点存到栈里
2. 访问（指针指向）左子树
3. 输出左子树（后面想了想又觉得不对，如果这样的话无论如何第一个输出的都是第二层的左孩子）

（根）结点为空：

1. 输出上一层的根结点（位于栈顶）
2. 指针指向根结点的右子树

Project 1：

Status InOrderTraverse(BiTree T)
{BiTree p=T;//用于访问结点的指针SqStack S;InitStack(S);if (p)//p不为空,有（根）结点//另外这里注意，我们无法构造定义出“空结点/空树”，不要浪费力气了{Push(S, p->data);//		把根结点存到栈里p->lchild;//		访问（指针指向）左子树}else//（根）结点为空{Pop(S, p->data);cout << p->data;//		输出上一层的根节点（位于栈顶）p = p->rchild;//指针指向根节点的右子树}return true;	
}

ISSUES:

一、还需要在：

最后加上一个限定条件，判定程序结束（停止退出循环）：

所有节点都输出完毕了，程序即停止运行，也就是说：

栈为空，且指针为空

二、是否有必要再构造新变量q，存放出栈的根结点？

是否必须如同（和）PPT答案一样，再构造一个变量来存放出栈时的那个根结点？

如果不这样像上述Project 1一样的话：

我感觉好像没什么问题：

Pop的过程中p原来的值被覆盖掉了，但是两种写法最终结果好像都是p指向右子树

但是这种都是自己的猜测，存疑，希望大家看看有没有问题

不过（另外）值得一提的是：

不构造新变量q会出现以下警告：【如果构造新变量q，则不会出现以下警告】

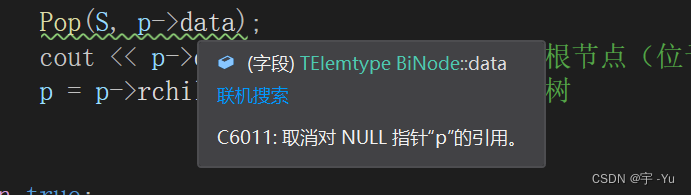
不构造新变量的最终程序成品：

Status InOrderTraverse(BiTree T)
{BiTree p = T;//用于访问结点的指针SqStack S;InitStack(S);while (p || StackEmpty(S)){if (p)//p不为空,有（根）结点//另外这里注意，我们无法构造定义出“空结点/空树”，不要浪费力气了{Push(S, p->data);//		把根结点存到栈里p->lchild;//		访问（指针指向）左子树}else//（根）结点为空{Pop(S, p->data);cout << p->data;//		输出上一层的根节点（位于栈顶）p = p->rchild;//指针指向根节点的右子树}}	return true;	
}

构造新变量的最终程序成品：(标准答案)

Status InOrderTraverse(BiTree T)
{BiTree p = T;SqStack S;InitStack(S);while (p || StackEmpty(S)){if (p){Push(S, p->data);p->lchild;}else{BiTree q = NULL;Pop(S, q->data);cout << q->data;p = q->rchild;}}	return true;	
}

注释版本：

Status InOrderTraverse(BiTree T)
{BiTree p = T;//用于访问结点的指针SqStack S;InitStack(S);while (p || StackEmpty(S)){if (p)//p不为空,有（根）结点//另外这里注意，我们无法构造定义出“空结点/空树”，不要浪费力气了{Push(S, p->data);//		把根结点存到栈里p->lchild;//		访问（指针指向）左子树}else//（根）结点为空{BiTree q = NULL;//用于访问结点的指针Pop(S, q->data);cout << q->data;//		输出上一层的根节点（位于栈顶）p = q->rchild;//指针指向根节点的右子树}}	return true;	
}