目录

前言

文献阅读

背景

需要改进的方向

主要思路

模型开发

CNN 和 LSTM 之间的耦合 

多任务学习

物理可解释性方法

实验数据（指标）

评估指标 

克里金插值python代码实战

总结

前言

 This week, I learned an article that used CNN and LSTM to establish a spatiotemporal DL based integrated model for hydrological simulation, and evaluated it in the source areas of the Yellow River, Yangtze River, and Lancang River. In addition, we use a simple linear regression method to explore the physical interpretability of CNN and LSTM in hydrological models based on deep learning (physical interpretability simply means defining unknown data), to improve our understanding of hydrological processes inferred from deep learning models. In terms of code, this week, learn how to use Python to solve practical problems with Kriging interpolation.

本周我学习了一篇文章，该研究通过耦合CNN和LSTM建立基于时空DL的集成模型进行水文模拟，并在黄河、长江和澜沧江源区进行了评估。此外，我们采用简单的线性回归方法探索基于深度学习的水文模型中CNN和LSTM的物理可解释性（物理可解释性简单来说就是给未知的数据下定义），以提高我们对深度学习模型推断水文过程的理解。在代码方面，本周学习如何用python解决克里金插值的实际问题。

文献阅读

--Bu Li, Ruidong Li, Ting Sun, Aofan Gong, Fuqiang Tian, Mohd Yawar Ali Khan, Guangheng Ni,
Improving LSTM hydrological modeling with spatiotemporal deep learning and multi-task learning: a case study of three mountainous areas on the Tibetan Plateau,
Journal of Hydrology,
2023,
129401,
ISSN 0022-1694,
https://doi.org/10.1016/j.jhydrol.2023.129401.

背景

水文模型，无论是基于物理的还是数据驱动的，在洪水和干旱灾害预防以及水资源管理中发挥着至关重要的作用。遥感和计算技术的最新进展通过增强其在更精细尺度上表征流体动力学过程的能力，改进了基于物理的水文模型。值得注意的是，分布式水文模型 （DHM） 可以纳入子流域或其他计算单位尺度的过程。然而，由于规模不匹配的未解决问题，DHM 的应用仍然有限。

数据驱动的模型可以直接描述输入和输出之间的统计关系，而无需明确描述物理过程。自 1990 年代以来，机器学习 （ML） 技术已广泛用于水文建模，并且与 DHM 相比，已证明具有相似或更好的性能。特别是，以神经网络为特色的深度学习 （DL） 模型是水文建模最常用的 ML 技术。它们已经从原始的多层感知器，即人工神经网络（ANN）发展到具有丰富分类法的更高级形式，例如卷积神经网络（CNNs）、递归神经网络（RNN）及其变体、长短期记忆网络（LSTM)。人工神经网络、CNN 和 RNN 是最早的 DL 模型之一，在水文建模方面具有良好的性能。作为前馈神经网络，ANN和CNN不能直接表示时间动态，因此无法准确表征水文过程。相比之下，按时间顺序处理输入数据的 RNN 可以考虑时间动态。尽管 RNN 更适合时间序列分析，但vanilla RNN 几乎无法存储超过 10 个时间步长的序列，这限制了它们在建模在较大时间尺度上发生的缓慢水文过程方面的适用性，例如与地下水、雪和冰川储存相关的过程。最近出现的LSTM模型可以通过独特的内部门架构克服这种弱点，并且在时间序列分析中表现出比vanilla RNN更好的性能。

需要改进的方向

当前基于 DL 的水文模型在水文建模方面很有前途，但在三个值得注意的方面仍需要改进：

(1)解析时空特征的能力：水文过程建模在很大程度上取决于气象强迫的空间模式和底层表面特征。Yang等人（2020）利用计算机视觉来解决ANN P-Q建模中的空间特征，并证明空间信息在增强模型鲁棒性方面起着重要作用。然而，大多数关于 LSTM 水文建模的现有研究几乎利用流域空间平均气象数据作为模型输入，而没有完全表示 LSTM 水文建模输入的空间特征。 耦合2-D CNN和LSTM有望通过同时考虑时间动力学和空间特征来弥合这种差距，CNN-LSTM已被证明在不同领域很有前途（例如，P临近预报和水质预测）。

(2)考虑多个水文过程：与基于物理的水文模型不同，基于LSTM的模型模拟单个水文过程，例如Q、地下水和雪水当量，但很少同时模拟多个过程。这使得基于 LSTM 的水文模型难以明确考虑不同水文过程之间的相互作用，也难以根据水文理论（例如水平衡方程）诊断模型。此外，一些研究发现，引入额外的水文过程，例如实际蒸发（表示为Ea一个在这项工作中）过程中，在基于物理的水文模型的校准中可以增强Q模拟性能。因此，研究基于LSTM的水文模型同时考虑多个水文过程是否可以提高其描绘更多水文过程的能力，从而提供更全面的水文变量诊断，这是有益的。

(3)物理可解释性：由于“黑匣子”性质，基于 DL 的水文模型没有明确表示物理过程，因此仍然受到一些水文学家的质疑。为了增强用户和政策制定者对采用基于深度学习的水文模型的信心，最近尝试提高对其物理可解释性的理解。例如，LSTM水文模型已被证明可以学习基础物理过程的可推广表示。LSTM 区域水文模型优于区域校准的 DHM，甚至针对每个盆地单独校准。 此外，发现 LSTM 水文模型能够存储与水文知识一致的隐藏信息。 然而，深度学习模型的物理可解释性相对于Ea一个过程 - 水文循环中的关键组成部分 - 还有待研究。此外，CNN-LSTM模型中CNN输出的物理概念仍不清楚。

主要思路

在这项工作中，我们旨在通过耦合2-D CNN和LSTM（CNN-LSTM）并引入多任务学习来开发基于时空DL的水文模型来克服这些缺陷。同时多任务（MT）学习在基于深度学习的水文模型中的潜力也通过参与Ea一个过程作为额外的学习目标。此外，我们还通过提取隐藏在所提出的LSTM和CNN-LSTM模型中的气象和水文过程，促进了对基于深度学习的模型的物理可解释性的理解。

模型开发

我们通过耦合1-D CNN（图2 b）和LSTM（图1 c）提出了基于DL的水文模型（图1a），以利用它们各自的优势：前者用于分层空间特征提取，而后者用于学习长时间依赖性。该模型可以使用二维空间气象和底层地表数据作为输入，并预测每日水文过程Q和Ea一个作为输出。然而，我们注意到每天只有气象数据。P和平均温度–在这项工作中使用，因为包含表面特征表明模型性能的改善很小（未显示）。该模型可以通过设置训练目标来执行单任务或多任务学习：前者模拟单个水文过程，而后者同时关注两个或多个过程。

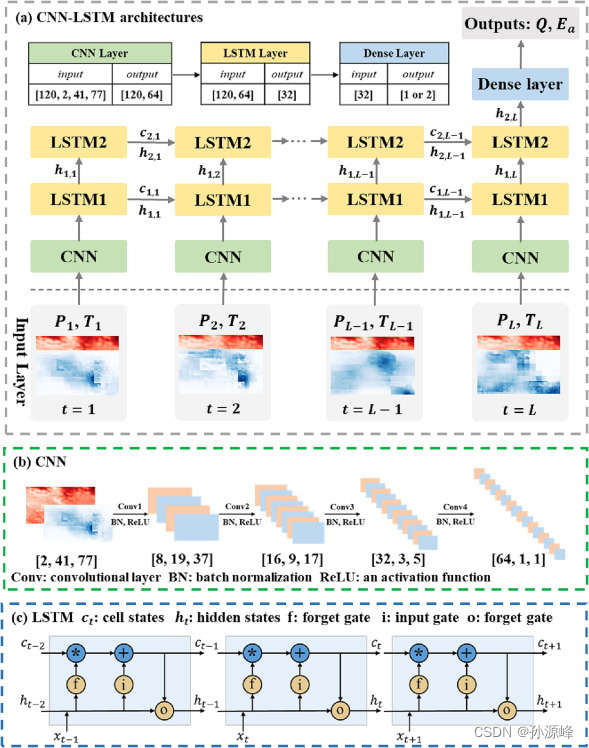
CNN 和 LSTM 之间的耦合 

为了利用CNN和LSTM模型的各自优势，我们通过耦合CNN和LSTM模型来开发基于时空DL的水文模型（图1a）。在每个时间步长，CNN-LSTM耦合通过两个阶段实现：

1)CNN将二维网格气象输入简化为一维序列，并将其馈送到LSTM2层;

2)LSTM1 层的隐藏状态被输入到 LSTM2 层，然后两个 LSTM 层的单元和隐藏状态分别在下一个时间步馈送到相应的层。

在时间步长之前通过CNN-LSTM耦合层进行所有处理后L，LSTM2 层在最后一个时间步的输出被传递到致密层以获得预测：学习的水文变量（图 1a）。根据目标模式（ST 或 MT），DL 模型可能会产生不同数量的输出变量。ST模型将一个水文过程设置为优化目标，而MT模型通过MT学习将两个或多个水文过程设置为优化目标。

多任务学习

多任务（MT）学习是在基于DL的模型中将多个任务设置为优化目标（Caruana 1997）。培训可以从MT信息的丰富表示中受益，从而使用其他任务中的信息来提高每个任务的性能。此外，与单任务 （ST） 学习相比，机器翻译学习可以实现更高的效率和更少的过度拟合，因为它可以将模型引导到多个相关任务首选的更通用的特征表示（Li 等人，2022 年，Li 等人，2023 年）。本文引入机器翻译学习，探讨多水文过程学习在基于LSTM的水文建模中的影响。

物理可解释性方法

DL 水文模型的内部嵌入层包含大量无法明确解释的数据。这些数据可能隐藏了一些未经训练的内部水文变量。例如，内部嵌入层Q模型可能包含有关Ea一个过程。本研究利用探针回归模型将训练模型的内部嵌入层映射到未经训练的水文变量（Hewitt 和 Liang，2019 年，Lees 等人，2022 年）——来测试经过训练的 DL 模型是否可以学习已知但未经训练的水文变量，并检查模型的内部表示和进一步的物理可解释性。最简单的探针形式是线性回归 （LR） 模型，它将学习的嵌入层连接到给定的输出。本研究基于LR模型，从提出的LSTM和CNN-LSTM模型中探索未经训练的水文变量。

实验数据（指标）

评估指标 

克里金插值python代码实战

(135条消息) python：克里金插值_python克里金插值__养乐多_的博客-CSDN博客

(135条消息) 【Python进阶】克里金插值法的实现过程_python克里金插值_指尖听戏的博客-CSDN博客

from gma.algorithm.spmis.interpolate import *class Kriging(IPolate):'''克里金法插值'''# 继承 gma 的标准插值类 IPolate。本处不再做详细说明。def __init__(self, Points, Values, Boundary = None, Resolution = None, InProjection = 'WGS84', VariogramModel = 'Linear',VariogramParameters = None,**kwargs):IPolate.__init__(self, Points, Values, Boundary, Resolution, InProjection)self.eps = eps# 初始化半变异函数及参数self.VariogramModel, self.VParametersList = GetVariogramParameters(VariogramModel, VariogramParameters)self.VariogramFUN = getattr(variogram, self.VariogramModel)if self.VParametersList is None:self.VParametersList = self._INITVariogramModel(**kwargs)# 调整输入数据if self.GType == 'PROJCS':self.Center = (self.Points.min(axis = 0) + self.Points.max(axis = 0)) * 0.5self.AnisotropyScaling = AnisotropyScalingself.AnisotropyAngle = AnisotropyAngleself.DistanceMethod = cdistelse:# 方便后期优化self.Center = np.array([0,0])self.AnisotropyScaling = 1.0self.AnisotropyAngle = 0.0self.DistanceMethod = GreatCircleDistanceself.AdjustPoints = AdjustAnisotropy(self.Points, self.Center, [self.AnisotropyScaling], [self.AnisotropyAngle])self.XYs = AdjustAnisotropy(self.XYs, self.Center,[self.AnisotropyScaling], [self.AnisotropyAngle])def _INITVariogramModel(self, **kwargs):'''初始化参数'''if 'NLags' in kwargs:NLags = kwargs['NLags']initialize.ValueType(NLags, 'pint')else:NLags = 6if 'Weight' in kwargs:Weight = ToNumericArray(kwargs['Weight']).flatten().astype(bool)[0]else:Weight = FalseLags, SEMI = INITVariogramModel(self.Points, self.Values, NLags, self.GType)# 为求解自动参数准备if self.VariogramModel == "Linear":X0 = [np.ptp(SEMI) / np.ptp(Lags), np.min(SEMI)]BNDS = ([0.0, 0.0], [np.inf, np.max(SEMI)])elif self.VariogramModel == "Power":X0 = [np.ptp(SEMI) / np.ptp(Lags), 1.1, np.min(SEMI)]BNDS = ([0.0, 0.001, 0.0], [np.inf, 1.999, np.max(SEMI)])else:X0 = [np.ptp(SEMI), 0.25 * np.max(Lags),  np.min(SEMI)]BNDS = ([0.0, 0.0, 0.0], [10.0 * np.max(SEMI), np.max(Lags), np.max(SEMI)])# 最小二乘法求解默认参数def _VariogramResiduals(Params, X, Y, Weight):if Weight:Weight = 1.0 / (1.0 + np.exp(-2.1972 / (0.1 * np.ptp(X)) * (0.7 * np.ptp(X) + np.min(X) - x))) + 1 else:Weight = 1return (self.VariogramFUN(X, *Params) - Y) * WeightRES = least_squares(_VariogramResiduals, X0, bounds = BNDS, loss = "soft_l1",args = (Lags, SEMI, Weight))return RES.xdef _GetKrigingMatrix(self):"""获取克里金矩阵"""LDs = self.DistanceMethod(self.AdjustPoints, self.AdjustPoints)A = -self.VariogramFUN(LDs, *self.VParametersList)A = np.pad(A, (0, 1), constant_values = 1)# 填充主对角线np.fill_diagonal(A, 0.0)return  Adef _UKExec(self, A, LDs, SearchRadius):"""泛克里金求解"""Args = LDs.argsort(axis = 1)[:,:SearchRadius]Values = self.Values[Args.T].T# A 的逆矩阵AInv = inv(A)B = -self.VariogramFUN(LDs, *self.VParametersList)B[np.abs(LDs) <= self.eps] = 0.0B = np.pad(B, ((0,0),(0,1)), constant_values = 1)X = np.dot(B, AInv)B = B[np.ogrid[:len(B)], Args.T].TX = X[np.ogrid[:len(X)], Args.T].TX = X / X.sum(axis = 1, keepdims = True)UKResults = np.sum(X * Values, axis = 1), np.sum((X * -B), axis = 1)return UKResultsdef _OKExec(self, A, LDs, SearchRadius):"""普通克里金求解"""Args = LDs.argsort(axis = 1)[:,:SearchRadius]LDs = LDs[np.ogrid[:len(LDs)], Args.T].TB = -self.VariogramFUN(LDs, *self.VParametersList)B[np.abs(LDs) <= self.eps] = 0.0B = np.pad(B, ((0,0),(0,1)), constant_values = 1)OKResults = np.zeros([2, len(LDs)])for i, b in enumerate(B):BSelector = Args[i] ASelector = np.append(BSelector, len(self.AdjustPoints))a = A[ASelector[:, None], ASelector]  x = solve(a, b)OKResults[:, i] = x[:SearchRadius].dot(self.Values[BSelector]), -x.dot(b)return OKResultsdef Execute(self, SearchRadius = 12, KMethod = 'Ordinary'):'''克里金插值'''initialize.ValueType(SearchRadius, 'pint')SearchRadius = np.min([SearchRadius, len(self.AdjustPoints)])A = self._GetKrigingMatrix()LDs = self.DistanceMethod(self.XYs, self.AdjustPoints)if KMethod not in ['Universal', 'Ordinary']:raise ValueError("Undefined Kriging method. Please select 'Universal' or 'Ordinary'!")elif KMethod == 'Universal':KResults = self._UKExec(A, LDs, SearchRadius)else:KResults = self._OKExec(A, LDs, SearchRadius)NT = namedtuple('Kriging', ['Data', 'SigmaSQ', 'Transform'])return NT(KResults[0].reshape(self.YLAT, self.XLON),KResults[1].reshape(self.YLAT, self.XLON), self.Transform)

总结

本周的计划是先会使用克里金插值解决简单问题，然后再查看克里金的包，查找他们之间的具体联系。