问题：现有n+1n+1n+1个2维的离散点Pi=(xi,yi),(i=0,1,⋯,n){P_i} = \left( {{x_i},{y_i}} \right),\left( {i = 0,1, \cdots ,n} \right)Pi​=(xi​,yi​),(i=0,1,⋯,n), 如何用Pi{P_i}Pi​拟合一条平滑的曲线，最后将曲线分割成数条 2阶/3阶贝塞尔曲线，并保证这数条曲线段拼接处是连续的，即全局可导。

2阶Bezier	3阶Bezier

1 Bezier路径拟合

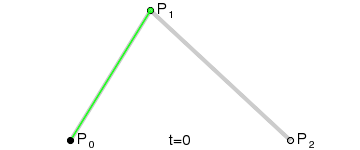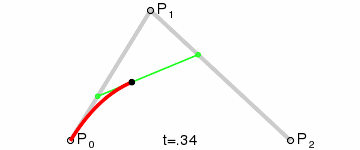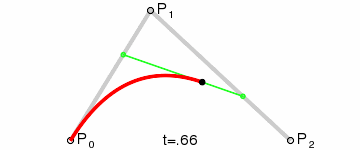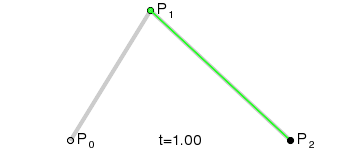
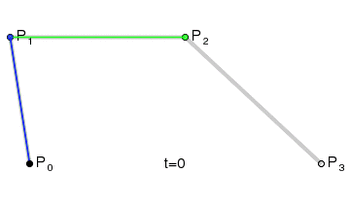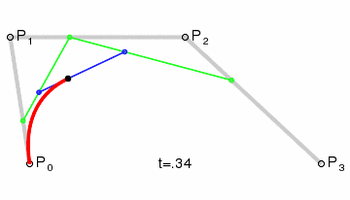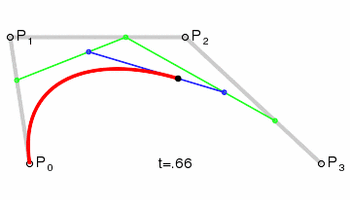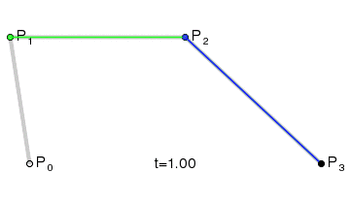
1.1 Bezier曲线绘制原理

Bezier曲线有两个简单的规律:
1、k阶的Bezier曲线需要用到k+1个数据点。 如: 3阶Bezier曲线需要用到4个数据点。
2、Berzier曲线只保证经过起点和终点，不保证经过中间所有的控制点。Berzier曲线用到的第1个数据点和倒数第1个数据点分别被称为起点和终点，中间的所有数据被称为控制点。

关注Pi{P_i}Pi​的4个数据点：
P0=(x0,y0),P1=(x1,y1),P2=(x2,y2),P3=(x3,y3){P_0} = \left( {{x_0},{y_0}} \right),{P_1} = \left( {{x_1},{y_1}} \right),{P_2} = \left( {{x_2},{y_2}} \right),{P_3} = \left( {{x_3},{y_3}} \right)P0​=(x0​,y0​),P1​=(x1​,y1​),P2​=(x2​,y2​),P3​=(x3​,y3​)

定义向量t≜0:δt:1t \triangleq 0:\delta t:1t≜0:δt:1（这是MatLAB的写法， δt\delta tδt决定曲线绘制精度）。
1阶、2阶、3阶和n阶的Bezier曲线公式分别如下：
B1st=(1−t)P0+tP1B2nd=(1−t)2P0+2(1−t)tP1+t2P2B3rd=(1−t)3P0+3(1−t)2tP1+3(1−t)t2P2+t3P3Bnth=∑i=0na(i)⋅(1−t)b(i)⋅tc(i)⋅Pi(1)\begin{aligned}{B_{1st}} &= \left( {1 - t} \right){P_0} + t{P_1}\\ {B_{2nd}} &= {\left( {1 - t} \right)^2}{P_0} + 2\left( {1 - t} \right)t{P_1} + {t^2}{P_2}\\ {B_{3rd}} &= {\left( {1 - t} \right)^3}{P_0} + 3{\left( {1 - t} \right)^2}t{P_1} + 3\left( {1 - t} \right){t^2}{P_2} + {t^3}{P_3}\\ {B_{nth}} &= \sum\limits_{i = 0}^n {a\left( i \right) \cdot {{\left( {1 - t} \right)}^{b\left( i \right)}} \cdot {t^{c\left( i \right)}} \cdot {P_i}}\end{aligned} \tag{1}B1st​B2nd​B3rd​Bnth​​=(1−t)P0​+tP1​=(1−t)2P0​+2(1−t)tP1​+t2P2​=(1−t)3P0​+3(1−t)2tP1​+3(1−t)t2P2​+t3P3​=i=0∑n​a(i)⋅(1−t)b(i)⋅tc(i)⋅Pi​​(1)

其中，
{a(i)=n+1阶杨辉三角第n+1行的第i+1列的数b(i)=n−i;c(i)=i\left\{ \begin{aligned} a\left( i \right) &= {\text{ }}n + 1 阶杨辉三角第n+1行的第i+1列的数 \\ b\left( i \right) &= n - i;c\left( i \right) = i \\ \end{aligned} \right.{a(i)b(i)​= n+1阶杨辉三角第n+1行的第i+1列的数=n−i;c(i)=i​

下面给出计算n+1n+1n+1阶杨辉三角矩阵的Matlab代码

clear all; close all; clc;
n = 5;
YH = zeros(n+1,n+1);
for i = 1:1:n+1YH(i,1) = 1; % 第1列元素YH(i,i) = 1; % 对角线元素
endfor i = 3:1:n+1 % 从第三行开始，因为前两行都是1for j = 2:1:i-1 % 第1列和第i列已经都被赋值为1了YH(i,j) = YH(i-1,j-1) + YH(i-1,j);end
enda = YH(n+1,:) % 取n+1行作为系数% 运行结果 
% n = 0;	1
% n = 1;	1     1
% n = 2;	1     2     1
% n = 3;	1     3     3     1
% n = 4;	1     4     6     4     1
% n = 5;	1     5    10    10     5     1

1.2 基于Bezier曲线的路径拟合实验

2阶Bezier曲线绘制如下：

3阶Bezier曲线绘制如下：

n阶-Bezier曲线绘制如下 （n = 10）

实验结果分析：
1、对于n+1n+1n+1个离散数据点，用nnn阶的Bezier曲线来路径拟合并不是一个好的选择，很明显，上图的拟合效果很差；
2、用nnn阶Bezier曲线路径拟合会导致运算量暴增，阶次爆炸。
3、除计算量问题外，根据Bezier本身的原理，我们也是无法直接把nnn阶Bezier分割成多个2阶/3阶的贝塞尔曲线的。

要解决本文所提问题，我们只能通过其他的曲线拟合方法先实现路径拟合，然后再把它分割转换成2阶/3阶贝塞尔曲线的描述方式。下面将会介绍BSpline和Catmull_ROM两种曲线拟合方法。

2 BSpline路径拟合-分段拼接

通过调研发现，用BSpline曲线来拟合路径，是可以采用分段拼接的方式的，而且它可以保证拼接处是连续的，即全局可导。

2.1 Bspline曲线绘制原理

BSpline曲线有两个简单的规律:
1、k阶的BSpline曲线需要用到k+1个数据点。 如: 3阶BSpline曲线需要用到4个数据点。
2、BSpline曲线的特点是不经过任何数据点（这让我觉得用这个东西搞路径拟合有点离谱）

关注Pi{P_i}Pi​的4个数据点：
P0=(x0,y0),P1=(x1,y1),P2=(x2,y2),P3=(x3,y3){P_0} = \left( {{x_0},{y_0}} \right),{P_1} = \left( {{x_1},{y_1}} \right),{P_2} = \left( {{x_2},{y_2}} \right),{P_3} = \left( {{x_3},{y_3}} \right)P0​=(x0​,y0​),P1​=(x1​,y1​),P2​=(x2​,y2​),P3​=(x3​,y3​)

定义向量t≜0:δt:1t \triangleq 0:\delta t:1t≜0:δt:1（这是MatLAB的写法， δt\delta tδt决定曲线绘制精度）。
2阶BSpline拟合公式：
{a0=12(x0+x1)a1=x1−x0a2=12(x0−2x1+x2),{b0=12(y0+y1)b1=y1−y0b2=12(y0−2y1+y2)(2)\left\{ \begin{aligned} {a_0} &= \frac{1}{2}\left( {{x_0} + {x_1}} \right) \\ {a_1} &= {x_1} - {x_0} \\ {a_2} &= \frac{1}{2}\left( {{x_0} - 2{x_1} + {x_2}} \right) \\ \end{aligned} \right.,\left\{ \begin{aligned} {b_0} &= \frac{1}{2}\left( {{y_0} + {y_1}} \right) \\ {b_1} &= {y_1} - {y_0} \\ {b_2} &= \frac{1}{2}\left( {{y_0} - 2{y_1} + {y_2}} \right) \\ \end{aligned} \right.\tag{2}⎩⎨⎧​a0​a1​a2​​=21​(x0​+x1​)=x1​−x0​=21​(x0​−2x1​+x2​)​,⎩⎨⎧​b0​b1​b2​​=21​(y0​+y1​)=y1​−y0​=21​(y0​−2y1​+y2​)​(2)

B(t)=(x(t),y(t))⇒{x(t)=a0+a1t+a2t2y(t)=b0+b1t+b2t2(3)B\left( t \right) = \left( {x\left( t \right),y\left( t \right)} \right) \Rightarrow \left\{ \begin{aligned} x\left( t \right) &= {a_0} + {a_1}t + {a_2}{t^2} \\ y\left( t \right) &= {b_0} + {b_1}t + {b_2}{t^2} \\ \end{aligned} \right.\tag{3}B(t)=(x(t),y(t))⇒{x(t)y(t)​=a0​+a1​t+a2​t2=b0​+b1​t+b2​t2​(3)

3阶BSpline拟合公式：
{a0=16(x0+4x1+x2)a1=−12(x0−x2)a2=12(x0−2x1+x2)a3=−16(x0−3x1+3x2−x3),{b0=16(y0+yx1+y2)b1=−12(y0−y2)b2=12(y0−2y1+y2)b3=−16(y0−3y1+3y2−y3)(4)\left\{ \begin{aligned} {a_0} &= \frac{1}{6}\left( {{x_0} + 4{x_1} + {x_2}} \right) \\ {a_1} &= - \frac{1}{2}\left( {{x_0} - {x_2}} \right) \\ {a_2} &= \frac{1}{2}\left( {{x_0} - 2{x_1} + {x_2}} \right) \\ {a_3} &= - \frac{1}{6}\left( {{x_0} - 3{x_1} + 3{x_2} - {x_3}} \right) \\ \end{aligned} \right.,\left\{ \begin{aligned} {b_0} &= \frac{1}{6}\left( {{y_0} + y{x_1} + {y_2}} \right) \\ {b_1} &= - \frac{1}{2}\left( {{y_0} - {y_2}} \right)\\ {b_2} &= \frac{1}{2}\left( {{y_0} - 2{y_1} + {y_2}} \right) \\ {b_3} &= - \frac{1}{6}\left( {{y_0} - 3{y_1} + 3{y_2} - {y_3}} \right) \\ \end{aligned} \right.\tag{4}⎩⎨⎧​a0​a1​a2​a3​​=61​(x0​+4x1​+x2​)=−21​(x0​−x2​)=21​(x0​−2x1​+x2​)=−61​(x0​−3x1​+3x2​−x3​)​,⎩⎨⎧​b0​b1​b2​b3​​=61​(y0​+yx1​+y2​)=−21​(y0​−y2​)=21​(y0​−2y1​+y2​)=−61​(y0​−3y1​+3y2​−y3​)​(4)

B(t)=(x(t),y(t))⇒{x(t)=a0+a1t+a2t2+a3t3y(t)=b0+b1t+b2t2+b3t3(5)B\left( t \right) = \left( {x\left( t \right),y\left( t \right)} \right) \Rightarrow \left\{ \begin{aligned} x\left( t \right) &= {a_0} + {a_1}t + {a_2}{t^2} + {a_3}{t^3} \\ y\left( t \right) &= {b_0} + {b_1}t + {b_2}{t^2} + {b_3}{t^3} \\ \end{aligned} \right.\tag{5}B(t)=(x(t),y(t))⇒{x(t)y(t)​=a0​+a1​t+a2​t2+a3​t3=b0​+b1​t+b2​t2+b3​t3​(5)

2.2 Bspline分段拼接方法

假设现在有待拟合的n+1个离散点Pi=(xi,yi),(i=0,1,⋯,n){P_i} = \left( {{x_i},{y_i}} \right),\left( {i = 0,1, \cdots ,n} \right)Pi​=(xi​,yi​),(i=0,1,⋯,n) ，采用2阶BSpline分段拼接拟合过程如下：
以P0,P1,P2{P_0},{P_1},{P_2}P0​,P1​,P2​为控制点绘制第1条2阶BSpline
以P1,P2,P3{P_1},{P_2},{P_3}P1​,P2​,P3​为控制点绘制第2条2阶BSpline
…
以Pn−2,Pn−1,Pn{P_{n-2}},{P_{n-1}},{P_{n}}Pn−2​,Pn−1​,Pn​为控制点绘制第n-1条2阶BSpline
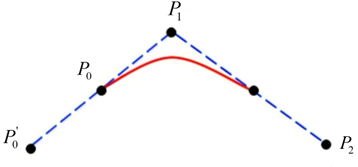
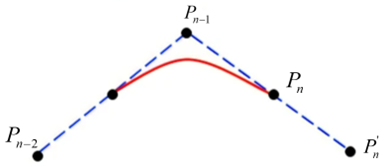
由于BSpline曲线不经过任何控制点，我们想让它经过第一个控制P0P_0P0​和最后一个PnP_ nPn​控制点 ，则需要修改P0P_0P0​和PnP_ nPn​。 注意2阶BSpline曲线与控制点相连线段相切于其中点。

P1−P0=P0−P0′⇒P0′=2P0−P1Pn′−Pn=Pn−Pn−1⇒Pn′=2Pn−Pn−1(6)\begin{aligned} {P_1} - {P_0} &= {P_0} - P_0' \Rightarrow P_0' = 2{P_0} - {P_1} \\ P_n' - {P_n} &= {P_n} - {P_{n - 1}} \Rightarrow P_n' = 2{P_n} - {P_{n - 1}} \\ \end{aligned}\tag{6}P1​−P0​Pn′​−Pn​​=P0​−P0′​⇒P0′​=2P0​−P1​=Pn​−Pn−1​⇒Pn′​=2Pn​−Pn−1​​(6)

假设现在有待拟合的n+1个离散点Pi=(xi,yi),(i=0,1,⋯,n){P_i} = \left( {{x_i},{y_i}} \right),\left( {i = 0,1, \cdots ,n} \right)Pi​=(xi​,yi​),(i=0,1,⋯,n) ，采用3阶BSpline分段拼接拟合过程如下：
以P0,P1,P2,P3{P_0},{P_1},{P_2},{P_3}P0​,P1​,P2​,P3​为控制点绘制第1条3阶BSpline
以P1,P2,P3,P4{P_1},{P_2},{P_3},{P_4}P1​,P2​,P3​,P4​为控制点绘制第2条3阶BSpline
…
以Pn−3,Pn−2,Pn−1,Pn{P_{n-3}},{P_{n-2}},{P_{n-1}},{P_{n}}Pn−3​,Pn−2​,Pn−1​,Pn​为控制点绘制第n-2条3阶BSpline
由于BSpline不经过任何控制点，我们想让它经过第一个控制P0P_0P0​和最后一个PnP_ nPn​控制点 ，则需要修改P0P_0P0​和PnP_ nPn​ 。 修改前先描述一下3阶BSpline曲线与控制点之间的关系。

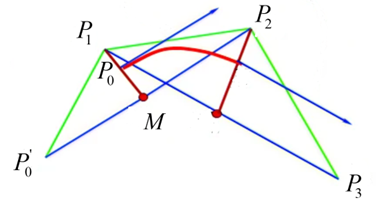
M1M_1M1​ 为P0P_0P0​和P2P_2P2​的中点， M2M_2M2​ 为P1P_1P1​和P3P_3P3​的中点, P1S=13P1M1{P_1}S = \frac{1}{3}{P_1}{M_1}P1​S=31​P1​M1​， P2E=13P2M2{P_2}E = \frac{1}{3}{P_2}{M_2}P2​E=31​P2​M2​, SE~\tilde{SE}SE~就是我们通过这4个控制点画出的3阶BSpline曲线。

现在修改为：

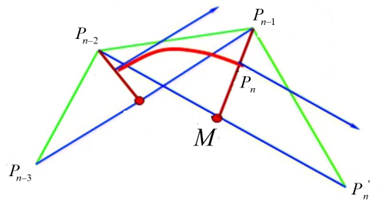
{M=12(P0′+P2)3(P0−P1)=M−P1⇒P0′=6P0−4P1−P2(7)\left\{ \begin{aligned} M &= \frac{1}{2}\left( {P_0' + {P_2}} \right)\\ 3\left( {{P_0} - {P_1}} \right) &= M - {P_1} \end{aligned} \right. \Rightarrow P_0' = 6{P_0} - 4{P_1} - {P_2}\tag{7}⎩⎨⎧​M3(P0​−P1​)​=21​(P0′​+P2​)=M−P1​​⇒P0′​=6P0​−4P1​−P2​(7)

同理，
Pn′=6Pn−4Pn−1−Pn−2(8)P_n' = 6{P_n} - 4{P_{n - 1}} - {P_{n - 2}}\tag{8}Pn′​=6Pn​−4Pn−1​−Pn−2​(8)

2.3 基于BSpline曲线的路径拟合实验

2阶BSpline

2阶Bspline拟合11个数据点（不修改P0和Pn点，双击图片可放大看细节）

2阶Bspline拟合11个数据点（修改P0和Pn点，双击图片可放大看细节）

3阶BSpline

3阶Bspline拟合11个数据点（不修改P0和Pn点，双击图片可放大看细节）

3阶Bspline拟合11个数据点（修改P0和Pn点，双击图片可放大看细节）

实验结果分析：
1、验证了BSpline用分段拼接拟合的可行性，很明显，拟合曲线是全局可导的；
2、拟合精度明显比n阶的Bezier曲线要高。对于n+1n+1n+1个离散数据点，现在我们已经用n−1n-1n−1条的2阶BSpline曲线或者n−2n-2n−2条的3阶BSpline曲线拼接拟合，完成。

现在的问题是如何将2阶和3阶的BSpline曲线用Bezier曲线的描述。

2.4 BSpline To Bezier

以2阶为例

2阶Bezier公式如下
B2nd=(1−t)2P0+2(1−t)tP1+t2P2{B_{2nd}} = {\left( {1 - t} \right)^2}{P_0} + 2\left( {1 - t} \right)t{P_1} + {t^2}{P_2}B2nd​=(1−t)2P0​+2(1−t)tP1​+t2P2​

2阶BSpline公式如下
{a0=12(x0+x1)a1=x1−x0a2=12(x0−2x1+x2),{b0=12(y0+y1)b1=y1−y0b2=12(y0−2y1+y2)\left\{ \begin{aligned} {a_0} &= \frac{1}{2}\left( {{x_0} + {x_1}} \right) \\ {a_1} &= {x_1} - {x_0} \\ {a_2} &= \frac{1}{2}\left( {{x_0} - 2{x_1} + {x_2}} \right) \\ \end{aligned} \right.,\left\{ \begin{aligned} {b_0} &= \frac{1}{2}\left( {{y_0} + {y_1}} \right) \\ {b_1} &= {y_1} - {y_0} \\ {b_2} &= \frac{1}{2}\left( {{y_0} - 2{y_1} + {y_2}} \right) \\ \end{aligned} \right.⎩⎨⎧​a0​a1​a2​​=21​(x0​+x1​)=x1​−x0​=21​(x0​−2x1​+x2​)​,⎩⎨⎧​b0​b1​b2​​=21​(y0​+y1​)=y1​−y0​=21​(y0​−2y1​+y2​)​

B(t)=(x(t),y(t))⇒{x(t)=a0+a1t+a2t2y(t)=b0+b1t+b2t2B\left( t \right) = \left( {x\left( t \right),y\left( t \right)} \right) \Rightarrow \left\{ \begin{aligned} x\left( t \right) &= {a_0} + {a_1}t + {a_2}{t^2} \\ y\left( t \right) &= {b_0} + {b_1}t + {b_2}{t^2} \\ \end{aligned} \right.B(t)=(x(t),y(t))⇒{x(t)y(t)​=a0​+a1​t+a2​t2=b0​+b1​t+b2​t2​

观察规律， 无论Bezier还是BSpline都是关于ttt的2阶线性函数，因此从原理上他们是可以完全等价的。观察Bezier的公式，ttt的系数完全由控制点P0,P1,P2{P_0},{P_1},{P_2}P0​,P1​,P2​确定，也就是说3个控制可以唯一确定一条2阶的Bezier曲线，那么我们只要求出P0,P1,P2{P_0},{P_1},{P_2}P0​,P1​,P2​就完成了BSpline到Bezier的转换。
令B(t)=B2ndB\left( t \right) = {B_{2nd}}B(t)=B2nd​，让ttt的各阶系数分别相等，即可推导出P0,P1,P2{P_0},{P_1},{P_2}P0​,P1​,P2​用a0,a1,a2,b0,b1,b2{a_0},{a_1},{a_2},{b_0},{b_1},{b_2}a0​,a1​,a2​,b0​,b1​,b2​表示的代数表达式:

{x0=a0x1=a0+12a1x2=a0+a1+a2,{y0=b0y1=b0+12b1y2=b0+b1+b2(9)\left\{ \begin{array}{l} {x_0} = {a_0}\\\\ {x_1} = {a_0} + \frac{1}{2}{a_1}\\\\ {x_2} = {a_0} + {a_1} + {a_2} \end{array} \right.,\left\{ \begin{array}{l} {y_0} = {b_0}\\\\ {y_1} = {b_0} + \frac{1}{2}{b_1}\\\\ {y_2} = {b_0} + {b_1} + {b_2} \end{array} \right.\tag{9}⎩⎨⎧​x0​=a0​x1​=a0​+21​a1​x2​=a0​+a1​+a2​​,⎩⎨⎧​y0​=b0​y1​=b0​+21​b1​y2​=b0​+b1​+b2​​(9)

P0=(x0,y0),P1=(x1,y1),P2=(x2,y2)(10){P_0} = \left( {{x_0},{y_0}} \right),{P_1} = \left( {{x_1},{y_1}} \right),{P_2} = \left( {{x_2},{y_2}} \right)\tag{10}P0​=(x0​,y0​),P1​=(x1​,y1​),P2​=(x2​,y2​)(10)

注意：这里的P0=(x0,y0){P_0} = \left( {{x_0},{y_0}} \right)P0​=(x0​,y0​)，并不是原始的需要拟合的数据点。而是用Bezier来等价描述BSpline的数据点。

同理，3阶的转换公式如下：
{x0=a0x1=a0+13a1x2=a0+23a1+13a2x3=a0+a1+a2+a3,{y0=b0y1=b0+13b1y2=b0+23b1+13b2y3=b0+b1+b2+b3(11)\left\{ \begin{array}{l} {x_0} = {a_0}\\\\ {x_1} = {a_0} + \frac{1}{3}{a_1}\\\\ {x_2} = {a_0} + \frac{2}{3}{a_1} + \frac{1}{3}{a_2}\\\\ {x_3} = {a_0} + {a_1} + {a_2} + {a_3} \end{array} \right.,\left\{ \begin{array}{l} {y_0} = {b_0}\\\\ {y_1} = {b_0} + \frac{1}{3}{b_1}\\\\ {y_2} = {b_0} + \frac{2}{3}{b_1} + \frac{1}{3}{b_2}\\\\ {y_3} = {b_0} + {b_1} + {b_2} + {b_3} \end{array} \right.\tag{11}⎩⎨⎧​x0​=a0​x1​=a0​+31​a1​x2​=a0​+32​a1​+31​a2​x3​=a0​+a1​+a2​+a3​​,⎩⎨⎧​y0​=b0​y1​=b0​+31​b1​y2​=b0​+32​b1​+31​b2​y3​=b0​+b1​+b2​+b3​​(11)

P0=(x0,y0),P1=(x1,y1),P2=(x2,y2),P3=(x3,y3)(12){P_0} = \left( {{x_0},{y_0}} \right),{P_1} = \left( {{x_1},{y_1}} \right),{P_2} = \left( {{x_2},{y_2}} \right),{P_3} = \left( {{x_3},{y_3}} \right)\tag{12}P0​=(x0​,y0​),P1​=(x1​,y1​),P2​=(x2​,y2​),P3​=(x3​,y3​)(12)

基于BSpline的路径拟合到此结束，BSpline由于其包络性和平滑性，广泛应用于无人驾驶路径规划领域。但由于BSpline不经过任何数据点，在某些特殊情况下，并不适用，因此接下来我们介绍一种经过所有点的曲线拟合方式 Catmull_Rom。

3 Catmull_Rom路径拟合-分段拼接

通过调研发现，用Catmull_Rom曲线来拟合路径，也是可以采用分段拼接的方式的，而且它同样可以保证拼接处是连续的，即全局可导，而且它还有一个致命优势，那就是它可以经过所有用于拟合的数据点。

3.1 Catmull_Rom曲线绘制原理

Catmull_Rom曲线有两个特点:
1、Catmull_Rom是3阶线性拟合，至少需要4个数据点；
2、假设我现在用A B C D 4个数据点绘制Catmull_Rom曲线，曲线只会经过B C。

关注Pi{P_i}Pi​的4个数据点：
P0=(x0,y0),P1=(x1,y1),P2=(x2,y2),P3=(x3,y3){P_0} = \left( {{x_0},{y_0}} \right),{P_1} = \left( {{x_1},{y_1}} \right),{P_2} = \left( {{x_2},{y_2}} \right),{P_3} = \left( {{x_3},{y_3}} \right)P0​=(x0​,y0​),P1​=(x1​,y1​),P2​=(x2​,y2​),P3​=(x3​,y3​)

定义向量t≜0:δt:1t \triangleq 0:\delta t:1t≜0:δt:1（这是MatLAB的写法， δt\delta tδt决定曲线绘制精度）。
Catmull_Rom拟合公式：
{a0=x1a1=12(−x0+x2)a2=12(2x0−5x1+4x2−x3)a3=12(−x0+3x1−3x2+x3),{b0=y1b1=12(−y0+y2)b2=12(2y0−5y1+4y2−y3)b3=12(−y0+3y1−3y2+y3)(13)\left\{ \begin{array}{l} {a_0} = {x_1}\\\\ {a_1} = \frac{1}{2}\left( { - {x_0} + {x_2}} \right)\\\\ {a_2} = \frac{1}{2}\left( {2{x_0} - 5{x_1} + 4{x_2} - {x_3}} \right)\\\\ {a_3} = \frac{1}{2}\left( { - {x_0} + 3{x_1} - 3{x_2} + {x_3}} \right) \end{array} \right.,\left\{ \begin{array}{l} {b_0} = {y_1}\\\\ {b_1} = \frac{1}{2}\left( { - {y_0} + {y_2}} \right)\\\\ {b_2} = \frac{1}{2}\left( {2{y_0} - 5{y_1} + 4{y_2} - {y_3}} \right)\\\\ {b_3} = \frac{1}{2}\left( { - {y_0} + 3{y_1} - 3{y_2} + {y_3}} \right) \end{array} \right.\tag{13}⎩⎨⎧​a0​=x1​a1​=21​(−x0​+x2​)a2​=21​(2x0​−5x1​+4x2​−x3​)a3​=21​(−x0​+3x1​−3x2​+x3​)​,⎩⎨⎧​b0​=y1​b1​=21​(−y0​+y2​)b2​=21​(2y0​−5y1​+4y2​−y3​)b3​=21​(−y0​+3y1​−3y2​+y3​)​(13)

Catmull_Rom(t)=(x(t),y(t))⇒{x(t)=a0+a1t+a2t2+a3t3y(t)=b0+b1t+b2t2+b3t3(14)Catmull\_Rom\left( t \right) = \left( {x\left( t \right),y\left( t \right)} \right) \Rightarrow \left\{ \begin{array}{l} x\left( t \right) = {a_0} + {a_1}t + {a_2}{t^2} + {a_3}{t^3}\\\\ y\left( t \right) = {b_0} + {b_1}t + {b_2}{t^2} + {b_3}{t^3} \end{array} \right.\tag{14}Catmull_Rom(t)=(x(t),y(t))⇒⎩⎨⎧​x(t)=a0​+a1​t+a2​t2+a3​t3y(t)=b0​+b1​t+b2​t2+b3​t3​(14)

3.2 Catmull_Rom分段拼接方法

前面我们也提到了，假设我现在用A B C D 4个数据点绘制Catmull_Rom曲线，曲线只会经过B C。如果我用B C D E个数据点绘制Catmull_Rom曲线,只会经过C D。如果想让拟合曲线经过所有控制点，则只需要分别在首和尾各添加一个控制点。
添加首尾两点的定义如下：

Ps≜(xs,ys),Pe≜(xe,ye)(15){P_s} \triangleq \left( {{x_s},{y_s}} \right),{P_e} \triangleq \left( {{x_e},{y_e}} \right)\tag{15}Ps​≜(xs​,ys​),Pe​≜(xe​,ye​)(15)

xs=x0+(x0−x1)ys=y0+(y0−y1)xe=xn+(xn−xn−1)ye=yn+(yn−yn−1)(16)\begin{aligned} {x_s} &= {x_0} + \left( {{x_0} - {x_1}} \right) \\ {y_s} &= {y_0} + \left( {{y_0} - {y_1}} \right) \\ {x_e} &= {x_n} + \left( {{x_n} - {x_{n - 1}}} \right)\\ {y_e} &= {y_n} + \left( {{y_n} - {y_{n - 1}}} \right) \end{aligned}\tag{16}xs​ys​xe​ye​​=x0​+(x0​−x1​)=y0​+(y0​−y1​)=xn​+(xn​−xn−1​)=yn​+(yn​−yn−1​)​(16)

以Ps,P0,P1,P2,P3,⋯,Pn,Pe{P_s},{P_0},{P_1},{P_2},{P_3}, \cdots ,{P_n},{P_e}Ps​,P0​,P1​,P2​,P3​,⋯,Pn​,Pe​为待拟合的数据点。

以Ps,P0,P1,P2{P_s},{P_0},{P_1},{P_2}Ps​,P0​,P1​,P2​绘制第1条Catmull_Rom曲线
以P0,P1,P2,P3{P_0},{P_1},{P_2},{P_3}P0​,P1​,P2​,P3​绘制第2条Catmull_Rom曲线
…
以Pn−2,Pn−1,Pn,Pe{P_{n-2}},{P_{n-1}},{P_n},{P_e}Pn−2​,Pn−1​,Pn​,Pe​为控制点绘制第n条Catmull_Rom曲线

3.3 基于Catmull_Rom曲线的路径拟合实验

直接上图

显然，Catmull_Rom曲线的拟合效果是很好的，对于数据点噪声较小的情况，是很适合用这种穿过所有数据点的曲线拟合方式的。

3.4 Catmull_Rom To Bezier

本质是 Catmull_Rom也是关于ttt的3阶线性函数，因此从原理上每一条Catmull_Rom曲线段是可以完全等价为3阶的Bezier曲线的。
Catmull_Rom和BSpline都是用a0,a1,a2,a3,b0,b1,b2,b3{a_0},{a_1},{a_2},{a_3},{b_0},{b_1},{b_2},{b_3}a0​,a1​,a2​,a3​,b0​,b1​,b2​,b3​作为系数，因此Catmull_Rom的转换公式和3阶BSpline的转换公式一样。
{x0=a0x1=a0+13a1x2=a0+23a1+13a2x3=a0+a1+a2+a3,{y0=b0y1=b0+13b1y2=b0+23b1+13b2y3=b0+b1+b2+b3(17)\left\{ \begin{array}{l} {x_0} = {a_0}\\\\ {x_1} = {a_0} + \frac{1}{3}{a_1}\\\\ {x_2} = {a_0} + \frac{2}{3}{a_1} + \frac{1}{3}{a_2}\\\\ {x_3} = {a_0} + {a_1} + {a_2} + {a_3} \end{array} \right.,\left\{ \begin{array}{l} {y_0} = {b_0}\\\\ {y_1} = {b_0} + \frac{1}{3}{b_1}\\\\ {y_2} = {b_0} + \frac{2}{3}{b_1} + \frac{1}{3}{b_2}\\\\ {y_3} = {b_0} + {b_1} + {b_2} + {b_3} \end{array} \right.\tag{17}⎩⎨⎧​x0​=a0​x1​=a0​+31​a1​x2​=a0​+32​a1​+31​a2​x3​=a0​+a1​+a2​+a3​​,⎩⎨⎧​y0​=b0​y1​=b0​+31​b1​y2​=b0​+32​b1​+31​b2​y3​=b0​+b1​+b2​+b3​​(17)

P0=(x0,y0),P1=(x1,y1),P2=(x2,y2),P3=(x3,y3)(18){P_0} = \left( {{x_0},{y_0}} \right),{P_1} = \left( {{x_1},{y_1}} \right),{P_2} = \left( {{x_2},{y_2}} \right),{P_3} = \left( {{x_3},{y_3}} \right)\tag{18}P0​=(x0​,y0​),P1​=(x1​,y1​),P2​=(x2​,y2​),P3​=(x3​,y3​)(18)

参考文献：

https://shenchunxu.blog.csdn.net/article/details/54411098?spm=1001.2014.3001.5506
https://zhuanlan.zhihu.com/p/137539722