二分查找

• 704. 二分查找
• 35. 搜索插入位置
• 34. 在排序数组中查找元素的第一个和最后一个位置
• 结语

704. 二分查找

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

链接: 二分查找

这个题是一个最基础的二分查找题目，需要你写出二分查找最基础的模板出来。
二分查找有许多的边界问题，每一次边界的处理都要坚持根据区间的定义来操作
，这就是循环不变量规则。

由题可知，该数组是一个升序的有序整型数组，

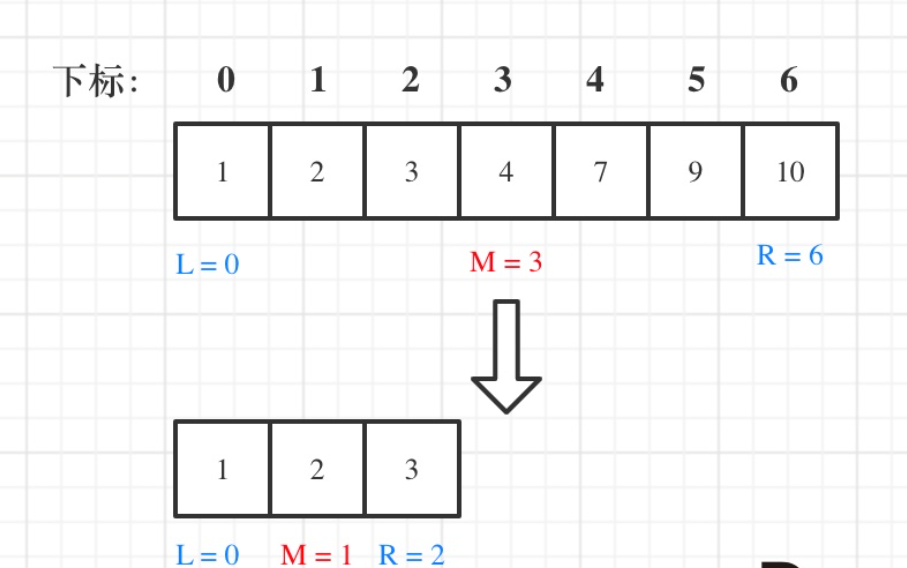
定义一个l变量，一个r变量，一个mid，分别表示的左值，右值，中值。
然后对每一次的mid中值进行一次check，当循环正常结束就是没有target值，
返回-1.

代码：

int search(int* nums, int numsSize, int target){int left=0,right=numsSize-1;int mid=(left+right)/2;while(leftif(nums[mid]>=target){right=mid;}else left=mid+1;mid=(left+right)/2;}if(nums[left]==target)return left;return -1;}

35. 搜索插入位置

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

输入: nums = [1,3,5,6], target = 5
输出: 2

输入: nums = [1,3,5,6], target = 2
输出: 1

输入: nums = [1,3,5,6], target = 7
输出: 4

链接: 搜索插入位置

这道题是二分查找的稍微进阶，相较于上一题需要考虑边界情况，
以及最后的返回值。

将上一题的代码拷贝下来

while(left<=right)
{if(nums[mid]==target){return mid;}if(nums[mid]>target){right=mid-1;}if(nums[mid]left=mid+1;}mid=(left+right)/2;

这是部分代码，从题中可知，
如果在遍历的时候找到与target对应的值，那么可以直接返回此时的下标mid
如果没有找到的话，循环结束后l，r，mid，这三个下标哪个是正确的返回值呢。

由题意得，返回的是按照值大小顺序插入的位置，所以返回了l的下标。

代码：

int searchInsert(int* nums, int numsSize, int target){int right =numsSize-1;int left=0;int mid=(right+left)/2;while(left<=right){if(nums[mid]==target){return mid;}if(nums[mid]>target){right=mid-1;}if(nums[mid]left=mid+1;}mid=(left+right)/2;}return left;}

34. 在排序数组中查找元素的第一个和最后一个位置

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

链接: 在排序数组中查找元素的第一个和最后一个位置

解题思路：
1.题目要求找出等于target大小的数组元素下标的开始位置和结束位置。
2.也就说需要进行两次二分查找，一次找出开始位置，一次找出结束位置
3.找出开始位置：

1. 当数组中有target元素的时候，我们可以将其分为两个部分
2. 第一个部分范围为所有 小于target的值
3. 第二部分则为所有 大于等于target的值
4. 由此可知，第二部分的开头位置的下标即为所求

代码：

        int l = 0;int r = nums.size() - 1;int mid = (l + r) / 2;while (l < r){if (nums[mid] >= target){r = mid;}else{l = mid + 1;}mid = (l + r) / 2;}

4.找出结束位置下标：（同上）

1. 当数组中有target元素的时候，我们可以将其分为两个部分
2. 第一个部分范围为所有 小于等于target的值
3. 第二部分则为所有 大于target的值
4. 由此可知，第一部分的结束位置的下标即为所求

注意： 此时随着循环更新的是l的值，所以更新方式应改变。mid=（l+r+1）/2
代码：

l = 0;
r = nums.size() - 1;
mid = (l + r+ 1) / 2;
while (l < r)
{if (nums[mid] <= target){l = mid;}else{r = mid - 1;}mid = (r + l+ 1) / 2;
}

每次求出也要检查所求下标对应的值是否为target。

代码：

class Solution {
public:vector searchRange(vector& nums, int target) {vector ans;//特殊情况处理if(nums.size()==0){ans.push_back(-1);ans.push_back(-1);return ans;}//初始位置int l = 0;int r = nums.size() - 1;int mid = (l + r) / 2;while (l < r){if (nums[mid] >= target){r = mid;}else{l = mid + 1;}mid = (l + r) / 2;}if (nums[l] == target) ans.push_back(l);else ans.push_back(-1);//结束位置l = 0;r = nums.size() - 1;mid = (l + r+ 1) / 2;while (l < r){if (nums[mid] <= target){l = mid;}else{r = mid - 1;}mid = (r + l+ 1) / 2;}if (nums[r] == target) ans.push_back(r);else ans.push_back(-1);return ans;}
};

结语

本期的二分查找到此结束，希望对各位有所帮助

我是Tom-猫
如果觉得有帮助的话，记得
一键三连哦ヾ(≧▽≦*)o。