1 信息量

意外越大，越不可能发生，概率就越小，信息量也就越大，也就是信息越多。比如说“今天肯定会天黑”，实现概率100%，说了和没说差不多，信息量就是0。
详见：2. 信息量

1.1 公式

I(x)=−logP(x)I(x)=-logP(x)I(x)=−logP(x)
概率P(x)越小，信息量越大，可以简单理解为最小编码长度，比如概率0.125，log(1/0.125)，如果以2为底做log，则需要3位二进制数描述。

2 熵

熵用于描述不确定性，越不确定，熵越高。熵是事件所属的整个分布的不确定性总量量化。可以说：熵越小，越容易被预测。

2.1 公式

H(x)=Ex∼P[I(x)]=−Ex∼P[log⁡P(x)]=−∑xP(x)log⁡P(x)H(\mathrm{x})=\mathbb{E}_{\mathbf{x} \sim P}[I(x)]=-\mathbb{E}_{\mathbf{x} \sim P}[\log P(x)]=-\sum_{x} P(x) \log P(x)H(x)=Ex∼P​[I(x)]=−Ex∼P​[logP(x)]=−x∑​P(x)logP(x)
这里乘了概率P(x)，等于计算了平均最小编码长度。

2.2 特性

• 接近均匀分布的概率分布具有较高的熵
• 接近确定性的分布 (输出几乎可以确定) 具有较低的熵

2.3 实例

import math
import scipy.statsarr = [1,10,100,1000]
e = 0
for x in arr:p = x/sum(arr)print(f"{x}, {round(p,5)} * {round(math.log(p),5)} = {round(p*math.log(p),5)}")e += p*math.log(p)
print(-e)
print(scipy.stats.entropy(arr))

运行结果

1, 0.0009 * -7.01302 = -0.00631
10, 0.009 * -4.71043 = -0.0424
100, 0.09001 * -2.40785 = -0.21673
1000, 0.90009 * -0.10526 = -0.09474
0.3601821726181299
0.3601821726181299

• 首先要注意的是：数组里存放的是每个类别中元素的个数，而不是元素的具体值，本例中共1111个元素，分为四类。
• p是每个类别出现的频率，取值在0-1之间，因此log§为负，频率p离1越近，log§离0越近。
• 就每一类而言，有以下几种可能：
  • a.该类占整体比例越大，p越大，log§离0越近，相乘后，对整体熵（混乱程度）的贡献比较小
  • b.该类占整体比例越小，p越小，log§离0越远，相乘后，对整体熵（混乱程度）的贡献比较小
  • c.该类占整体比例适中，p值中等，log§也中等，相乘后，对整体熵（混乱程度）的贡献反而比较大
• 其背后的逻辑是：
  • a.有一个类别可能性非常大（如a），绝大多数属于该类，就“蒙”这一类
  • b.有一个类别可能性非常小（如b），绝大多数不属于该类，“不蒙”这一类
  • c.如果数据被平均分成少数几个类别（c中的一种情况），那就很难“蒙对”了，这也是最不确定的情况

3 相对熵

相对熵可以用来衡量两个分布之间的差异程度。两者差异越小，KL散度越小。

3.1 KL散度

KL散度，KL距离，又叫相对熵(relative entropy)，衡量两个概率分布之间的不同程度。

• KL散度被称为：相对熵、互熵、鉴别信息、Kullback熵、Kullback-Leible散度(即KL散度的简写)。
• KL散度常在损失函数中用于限制函数变化。
• 在机器学习、深度学习领域中，KL散度被广泛运用于变分自编码器中(Variational AutoEncoder,简称VAE)、EM算法、GAN网络中。
• KL散度是非对称的，如需考虑双向散度，请见JS散度。
• KL散度结果为0-正无穷，很难给出一个绝对的阈值，但可以使用比较的方法计算相对的大小。

3.1.1 定义

一个离散随机变量X的可能取值为X=x1,x2,…xn，对应的概率pi=p(X=xi)。

3.1.2 离散公式

DKL(p∥q)=∑i=1np(x)log⁡p(x)q(x)D_{K L}(p \| q)=\sum_{i=1}^{n} p(x) \log \frac{p(x)}{q(x)}DKL​(p∥q)=i=1∑n​p(x)logq(x)p(x)​
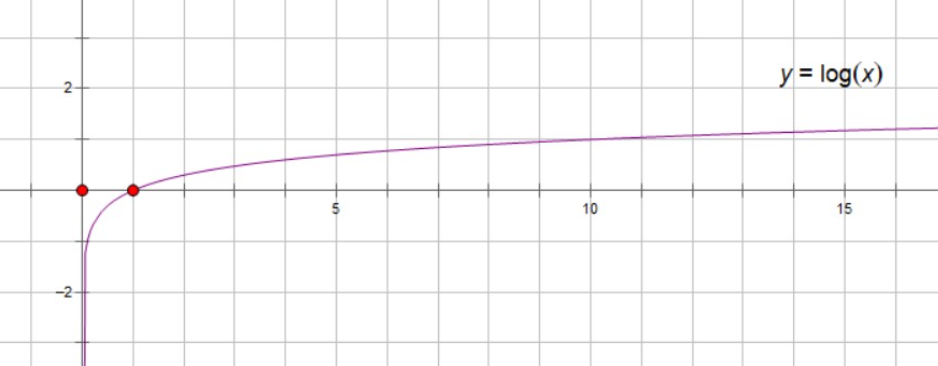
上述公式描述的是p相对于q的散度，针对每个x，计算不同分布中概率p(x)与q(x)的比值，当无差异时，其值为1，log(1)为0（见下方log函数图），此x项对应项则为0，否则根据其概率p(x)与差异的大小的乘积累加。当两个分布一致时，其KL散度为0。

3.1.3 连续公式

DKL(p∥q)=∫xp(x)log⁡p(x)q(x)dxD_{KL}(p \| q)=\int_x p(x) \log \frac{p(x)}{q(x)} d xDKL​(p∥q)=∫x​p(x)logq(x)p(x)​dx
与离散公式类似，差异是将离散x变为连续值计算积分，其目标也是让x取值范围中所有值p(x)与q(x)一致。

3.1.4 用途

• 用户画像
  使用KL散度去计算同一类型商品不同用户群体之间的金额（或其余指标）的KL散度，如果都很接近，说明这个类型商品不是不同用户群体之间的差异点，可以进行剔除，只保留有差异性的商品类型(KL散度较大)。

3.2 JS散度

3.2.1 定义

JS散度是基于KL散度的变体，解决了KL散度非对称的问题，同样是二者越相似，JS散度越小。

3.2.2 特性

JS散度的取值范围在0-1之间，完全相同时为0。

3.2.3 公式

JS(P1∣∣P2)=12KL(P1∣∣P1+P22)+12KL(P2∣∣P1+P22)J_S(P_1||P_2)=\frac{1}{2}KL(P_1||\frac{P_1+P_2}{2})+\frac{1}{2}KL(P_2||\frac{P_1+P_2}{2})JS​(P1​∣∣P2​)=21​KL(P1​∣∣2P1​+P2​​)+21​KL(P2​∣∣2P1​+P2​​)
把数据1和数据2放一块作为一个整体，再用数据1和数据2分别和整体比。

4 交叉熵

4.1 公式

交叉熵常作为损失函数使用，用于评价离散值的预测：
H(p,q)=∑xp(x)⋅log⁡(1q(x))\mathrm{H}(\mathrm{p}, \mathrm{q})=\sum_{x} p(x) \cdot \log \left(\frac{1}{q(x)}\right)H(p,q)=x∑​p(x)⋅log(q(x)1​)
p表示真实标签的分布，q则为训练后的模型的预测标签分布，交叉熵损失函数可以衡量p与q的相似性。如果把q换成p，则计算的是数据的熵。

4.2 交叉熵损失函数

交叉熵作为分类的损失函数时，由于实际上每个实例只属于一个分类，则只有一个p(x)为1，其它p(x)都为0，那么只需要考虑模型预测为该类别的概率q(x)。展开式示例如下：
H(P1,Q1)=−∑iP1(i)log⁡2Q1(i)=−(1log⁡0.4+0log⁡0.3+0log⁡0.05+0log⁡0.05+0log⁡0.2)≈0.916\begin{array}{c} H\left(P_{1}, Q_{1}\right)=-\sum_{i} P_{1}(i) \log _{2} Q_{1}(i) \\ =-(1 \log 0.4+0 \log 0.3+0 \log 0.05+0 \log 0.05+0 \log 0.2) \approx 0.916 \end{array} H(P1​,Q1​)=−∑i​P1​(i)log2​Q1​(i)=−(1log0.4+0log0.3+0log0.05+0log0.05+0log0.2)≈0.916​
当预测完全正确，q(x)=1，log(1/q(x))=0，p(x)=1，H(p,q)=0。
当预测概率为40%，q(x)=0.4，log(1/0.4)=0.916，p(x)=1，H(p,q)=0.916，预测不准，loss大。
当预测概率为90%，q(x)=0.9，log(1/0.9)=0.105，p(x)=1，H(p,q)=0.105，预测较准，loss小。
如果说第一项是“狗”，实际也真是狗，第一项的P(x)=1，也希望预测的q(x)接近1（它是个概率取值在0-1之间）；它离1越远(近0)，越要惩罚它。

5 参考

5.1 log曲线