文章目录

• 染色法判定二分图
• • [785. 判断二分图](https://leetcode.cn/problems/is-graph-bipartite/)
  • • 【重要】染色法(DFS)
  • [886. 可能的二分法](https://leetcode.cn/problems/possible-bipartition/)

染色法判定二分图

785. 判断二分图

难度中等449

存在一个 无向图 ，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：

• 不存在自环（graph[u] 不包含 u）。
• 不存在平行边（graph[u] 不包含重复值）。
• 如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
• 这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。

二分图 定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为 二分图 。

如果图是二分图，返回 true ；否则，返回 false 。

示例 1：

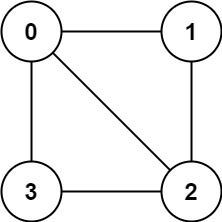
输入：graph = [[1,2,3],[0,2],[0,1,3],[0,2]]
输出：false
解释：不能将节点分割成两个独立的子集，以使每条边都连通一个子集中的一个节点与另一个子集中的一个节点。

示例 2：

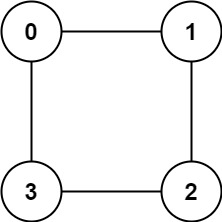
输入：graph = [[1,3],[0,2],[1,3],[0,2]]
输出：true
解释：可以将节点分成两组: {0, 2} 和 {1, 3} 。

提示：

• graph.length == n
• 1 <= n <= 100
• 0 <= graph[u].length < n
• 0 <= graph[u][i] <= n - 1
• graph[u] 不会包含 u
• graph[u] 的所有值 互不相同
• 如果 graph[u] 包含 v，那么 graph[v] 也会包含 u

【重要】染色法(DFS)

class Solution {ArrayList[] g;Map map;public boolean isBipartite(int[][] graph) {int n = graph.length;map = new HashMap<>();g = new ArrayList[n];for(int i = 0; i < n; i++) g[i] = new ArrayList();// 建图for(int i = 0; i < n; i++){for(int to : graph[i]){g[i].add(to);g[to].add(i);}}for(int i = 0; i < n; i++){// 如果当前节点还没有染色，尝试用颜色1对其染色，将相连的边都染成颜色2// 在对相邻边染色时，如果相邻节点颜色与节点i一致，则不符合规定，返回false ==> 最终结果就是falseif(!map.containsKey(i) && !dfs(i, 1)) return false;}return true;}// 返回true：能成功将idx染成color，能分成两个集合public boolean dfs(int idx, int color){if(map.containsKey(idx)) return map.get(idx) == color;map.put(idx, color);for(int e : g[idx]){if(!dfs(e, -color)) return false;}return true;}
}

886. 可能的二分法

难度中等365

给定一组 n 人（编号为 1, 2, ..., n）， 我们想把每个人分进任意大小的两组。每个人都可能不喜欢其他人，那么他们不应该属于同一组。

给定整数 n 和数组 dislikes ，其中 dislikes[i] = [ai, bi] ，表示不允许将编号为 ai 和 bi的人归入同一组。当可以用这种方法将所有人分进两组时，返回 true；否则返回 false。

示例 1：

输入：n = 4, dislikes = [[1,2],[1,3],[2,4]]
输出：true
解释：group1 [1,4], group2 [2,3]

示例 2：

输入：n = 3, dislikes = [[1,2],[1,3],[2,3]]
输出：false

示例 3：

输入：n = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
输出：false

提示：

• 1 <= n <= 2000
• 0 <= dislikes.length <= 104
• dislikes[i].length == 2
• 1 <= dislikes[i][j] <= n
• ai < bi
• dislikes 中每一组都 不同

题解：

我们用两种颜色对图进行染色，如果可以完成染色，那么就说明可以将所有人分进两组。

具体的染色方法如下：

• 初始化所有人的颜色为 0，表示还没有染色。
• 遍历所有人，如果当前人没有染色，那么就用颜色 1 对其进行染色，然后将其所有不喜欢的人用颜色 2 进行染色。如果染色过程中出现了冲突，那么就说明无法将所有人分进两组，返回 false。
• 如果所有人都染色成功，那么就说明可以将所有人分进两组，返回 true。

class Solution {ArrayList[] g;Map map;public boolean possibleBipartition(int n, int[][] dislikes) {g = new ArrayList[n];map = new HashMap<>();for(int i = 0; i < n; i++){g[i] = new ArrayList();}//建图for(int[] e : dislikes){g[e[0]-1].add(e[1]-1);g[e[1]-1].add(e[0]-1);}for(int i = 0; i < n; i++){if(!map.containsKey(i) && !dfs(i, 1)) return false;}return true;}public boolean dfs(int idx, int color){if(map.containsKey(idx)) return map.get(idx) == color;// 还没有染色，用颜色 1 染色map.put(idx, color);for(int next : g[idx]){// 将其所有不喜欢的人用颜色 2 进行染色if(!dfs(next, -color)) return false;}return true;}
}