基于 Zynq+AD+DA 的振动台控制器FPGA算法实现(三)
创始人
2025-06-01 20:21:33
4 振动台控制算法的 FPGA 实现
4.1 PID 控制算法
4.1.1 增量式 PID 控制算法
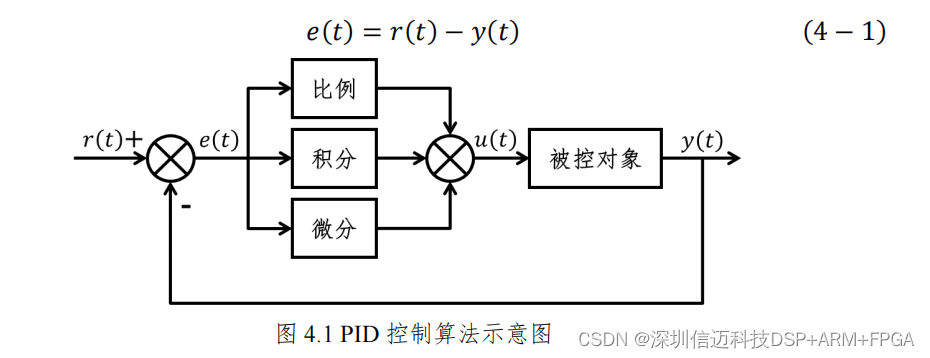
PID 控制为控制工程中经常使用的控制方法[33],其基本原理框图如图 4.1 所
示,其中𝑢𝑢(𝑡𝑡)为控制信号、𝑟𝑟(𝑡𝑡)为系统输入信号、𝑦𝑦(𝑡𝑡)为系统输出信号。控制系
统主要由比例(Proportional)、积分(Integral)和微分(Differential)三个环节组
成,系统误差经过控制器三个单元的运算和线性组合得到控制量,其中系统误差
𝑒𝑒(𝑡𝑡)可表示为
 4.2.2 三参量控制算法的 MATLAB/Simulink 仿真 为验证三参量控制算法的可行性,并为之后的参数调整提供参考,在 MATLAB/Simulink 中进行仿真[44,45]。如图 4.5 所示。
4.2.2 三参量控制算法的 MATLAB/Simulink 仿真 为验证三参量控制算法的可行性,并为之后的参数调整提供参考,在 MATLAB/Simulink 中进行仿真[44,45]。如图 4.5 所示。 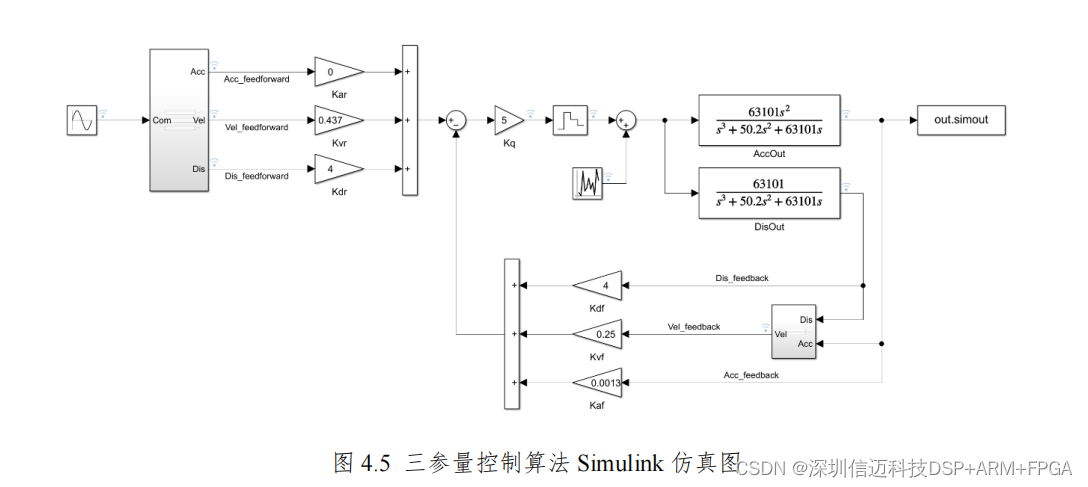
 4.2.3 三参量控制算法的 FPGA 实现 三参量控制算法的实现有两个关键点。一是速度反馈的合成,二是前馈量的 生成。前馈量可以由一种参考信号合成另外两个信号,也可以直接输入三个参考 信号,为方便起见,直接从地震数据库中下载了参考位移、参考速度和参考加速 度作为前馈信号输入到系统中。所以重点来讨论速度反馈的合成。 在振动台系统中,一般只有位移传感器和加速度传感器,所以需要用位移微 分或者加速度积分来合成速度[46–49]。这里采用两者结合的方式。由位移微分后再 低通滤波和加速度积分后再高通滤波,两者相加得到速度,如图 4.7 所示。具体 模块的实现框图如图 4.8。
4.2.3 三参量控制算法的 FPGA 实现 三参量控制算法的实现有两个关键点。一是速度反馈的合成,二是前馈量的 生成。前馈量可以由一种参考信号合成另外两个信号,也可以直接输入三个参考 信号,为方便起见,直接从地震数据库中下载了参考位移、参考速度和参考加速 度作为前馈信号输入到系统中。所以重点来讨论速度反馈的合成。 在振动台系统中,一般只有位移传感器和加速度传感器,所以需要用位移微 分或者加速度积分来合成速度[46–49]。这里采用两者结合的方式。由位移微分后再 低通滤波和加速度积分后再高通滤波,两者相加得到速度,如图 4.7 所示。具体 模块的实现框图如图 4.8。 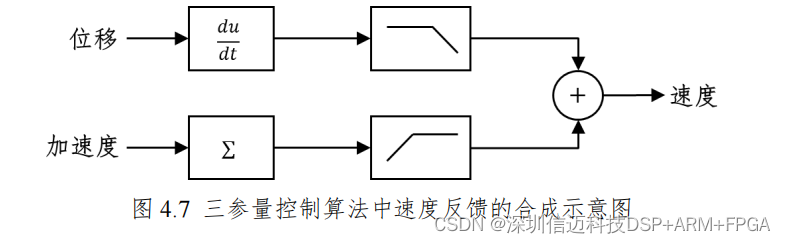



 4.2.2 三参量控制算法的 MATLAB/Simulink 仿真 为验证三参量控制算法的可行性,并为之后的参数调整提供参考,在 MATLAB/Simulink 中进行仿真[44,45]。如图 4.5 所示。
4.2.2 三参量控制算法的 MATLAB/Simulink 仿真 为验证三参量控制算法的可行性,并为之后的参数调整提供参考,在 MATLAB/Simulink 中进行仿真[44,45]。如图 4.5 所示。 
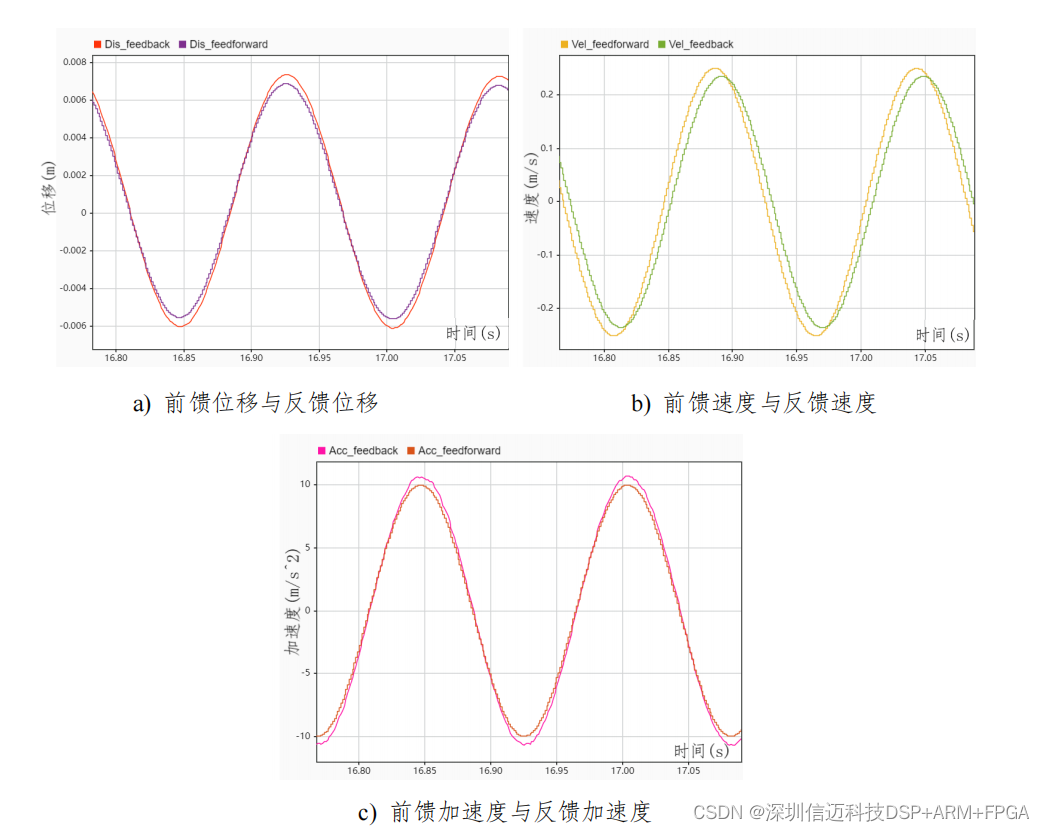
在输入的正弦波参考波形(加速度)幅值为 10,角频率为 40rad/s 时,得到 前馈与反馈的位移、速度、加速度波形如图 4.6 所示。
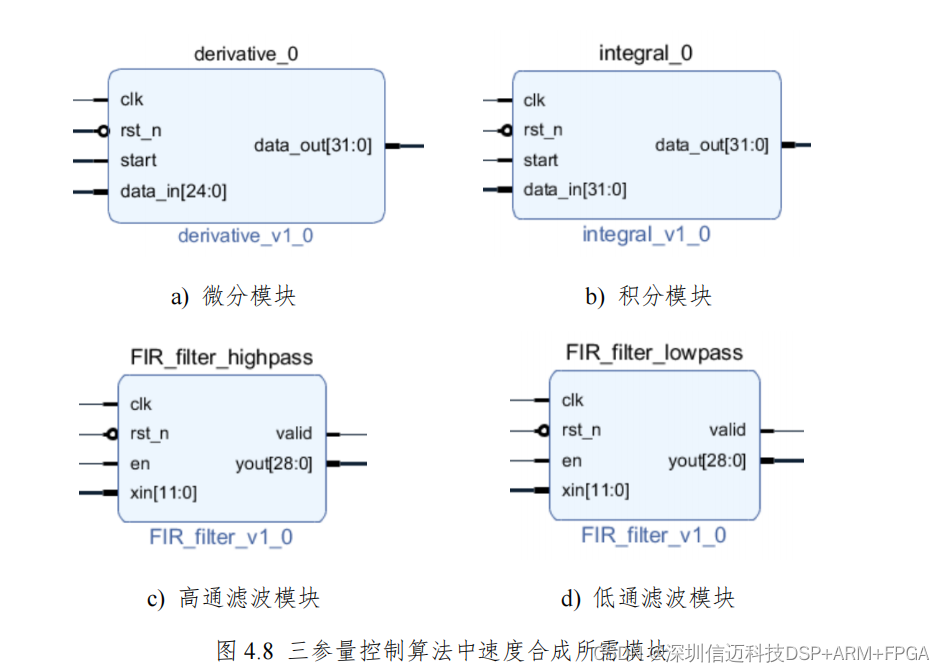
 4.2.3 三参量控制算法的 FPGA 实现 三参量控制算法的实现有两个关键点。一是速度反馈的合成,二是前馈量的 生成。前馈量可以由一种参考信号合成另外两个信号,也可以直接输入三个参考 信号,为方便起见,直接从地震数据库中下载了参考位移、参考速度和参考加速 度作为前馈信号输入到系统中。所以重点来讨论速度反馈的合成。 在振动台系统中,一般只有位移传感器和加速度传感器,所以需要用位移微 分或者加速度积分来合成速度[46–49]。这里采用两者结合的方式。由位移微分后再 低通滤波和加速度积分后再高通滤波,两者相加得到速度,如图 4.7 所示。具体 模块的实现框图如图 4.8。
4.2.3 三参量控制算法的 FPGA 实现 三参量控制算法的实现有两个关键点。一是速度反馈的合成,二是前馈量的 生成。前馈量可以由一种参考信号合成另外两个信号,也可以直接输入三个参考 信号,为方便起见,直接从地震数据库中下载了参考位移、参考速度和参考加速 度作为前馈信号输入到系统中。所以重点来讨论速度反馈的合成。 在振动台系统中,一般只有位移传感器和加速度传感器,所以需要用位移微 分或者加速度积分来合成速度[46–49]。这里采用两者结合的方式。由位移微分后再 低通滤波和加速度积分后再高通滤波,两者相加得到速度,如图 4.7 所示。具体 模块的实现框图如图 4.8。 
相关内容
热门资讯
【网络中国节·春节】春节假期温...
春节假期将至,蚌埠市文化旅游体育局温馨提醒广大游客,安全出行、文明旅游,共度祥和新春。 科学规划行程...
正定县旅游景点必玩推荐
正定县历史悠久,文化底蕴深厚,拥有众多独具特色的旅游景点,吸引着无数游客前来探寻。这里的每一处古迹都...
条条街巷皆是舞台、座座古建皆成...
央视网消息:2月16日就是除夕了,各地古城老街以新设计、新场景迎来了集体“上新”。福建莆田的兴化府历...
君行酒店:大湾区全品牌覆盖,打...
2026年春节,85国免签政策叠加9天超长假期,让“到中国过春节”成全球新风尚,入境游市场迎来爆发式...
