深度学习-【语义分割】学习笔记2 转置卷积（transposed convolution）
创始人
2025-05-30 00:34:05
0次

文章目录

  • 转置卷积
  • 运算步骤
  • 深入理解转置卷积

转置卷积

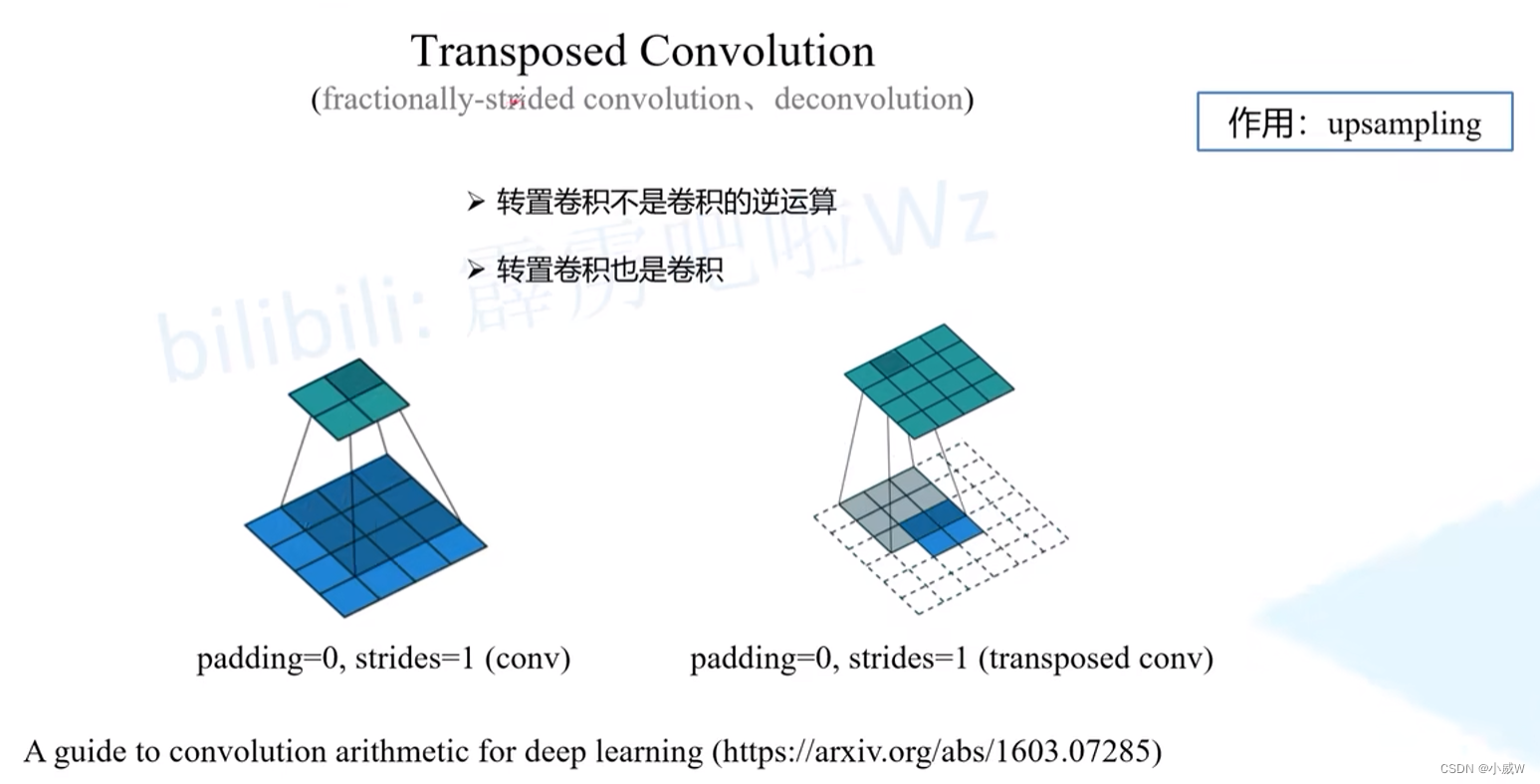
在这里插入图片描述
起到上采样的作用——shape从2×2变成4×4。

运算步骤

相关链接：https://github.com/vdumoulin/conv_arithmetic
在这里插入图片描述
先进行一些处理，再进行正常卷积的操作。

输出shape的计算，e.g. (3 - 1) * 2 - 2 * 1 + 3 = 5

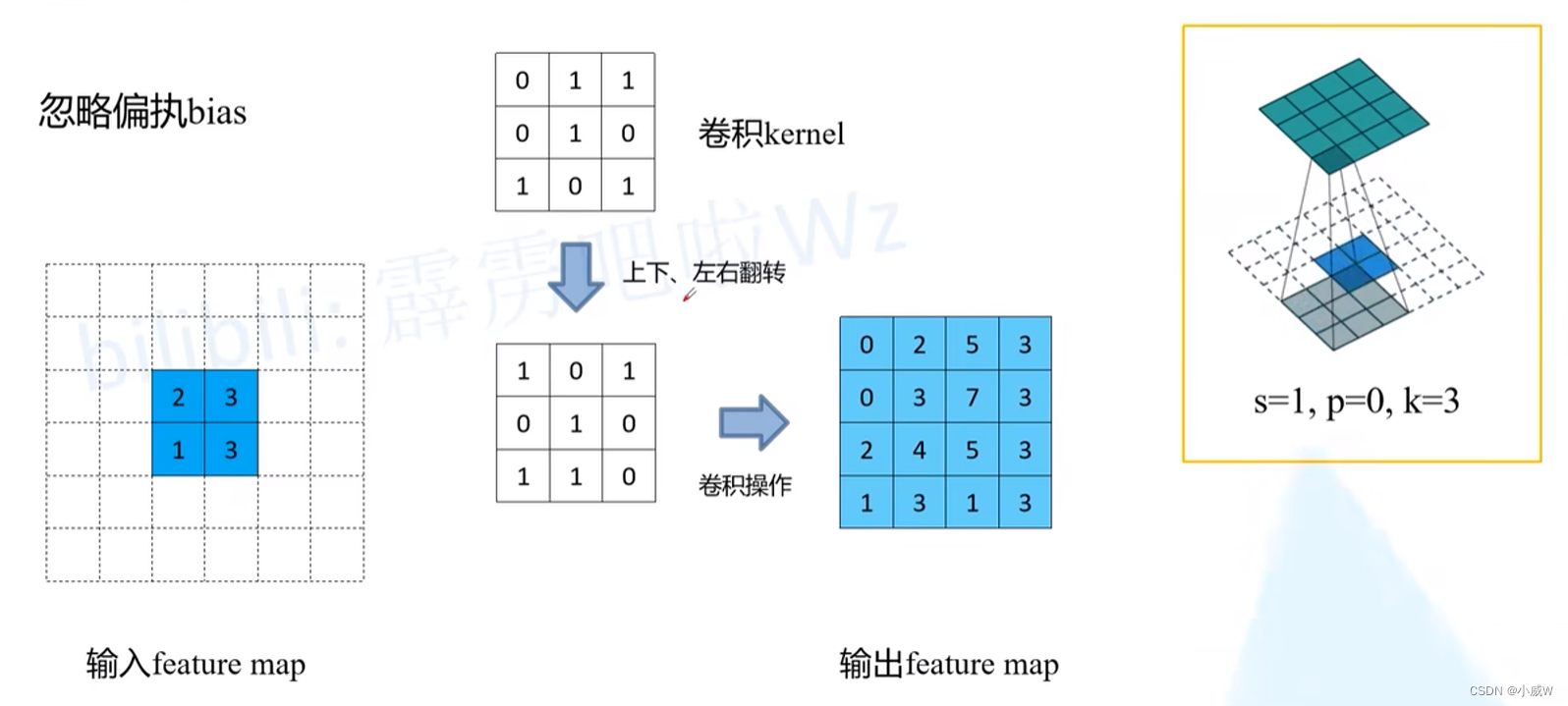
在这里插入图片描述

在这里插入图片描述

深入理解转置卷积

一个例子：
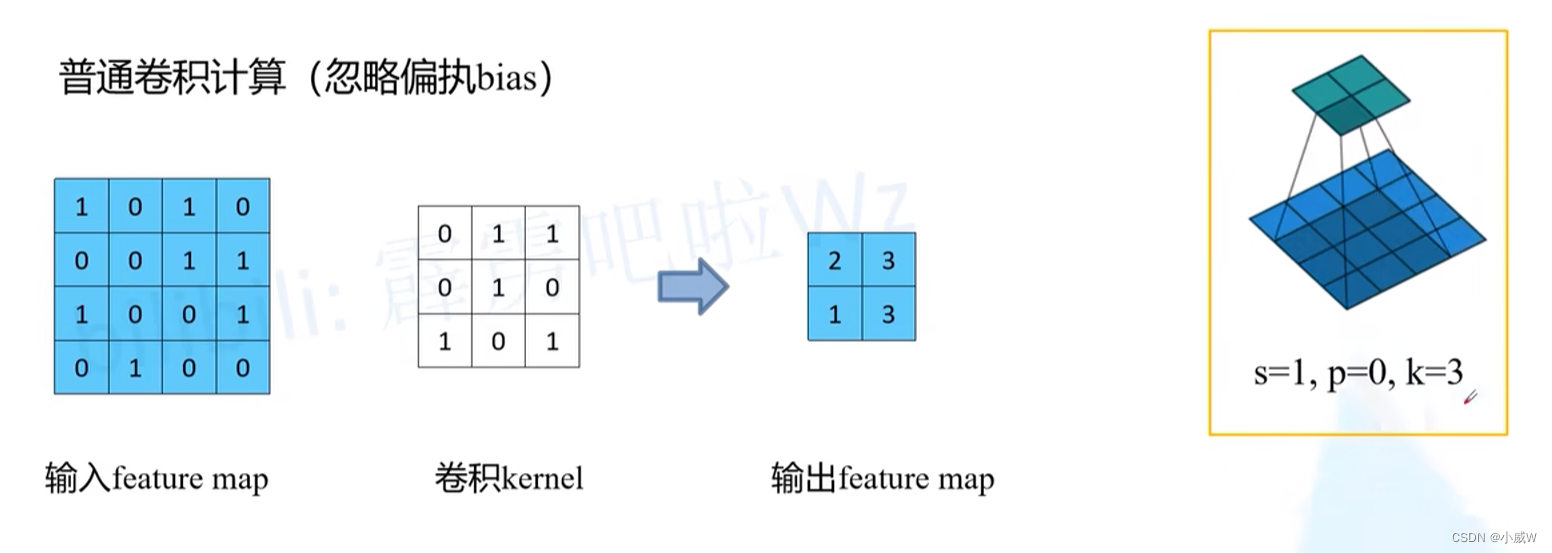
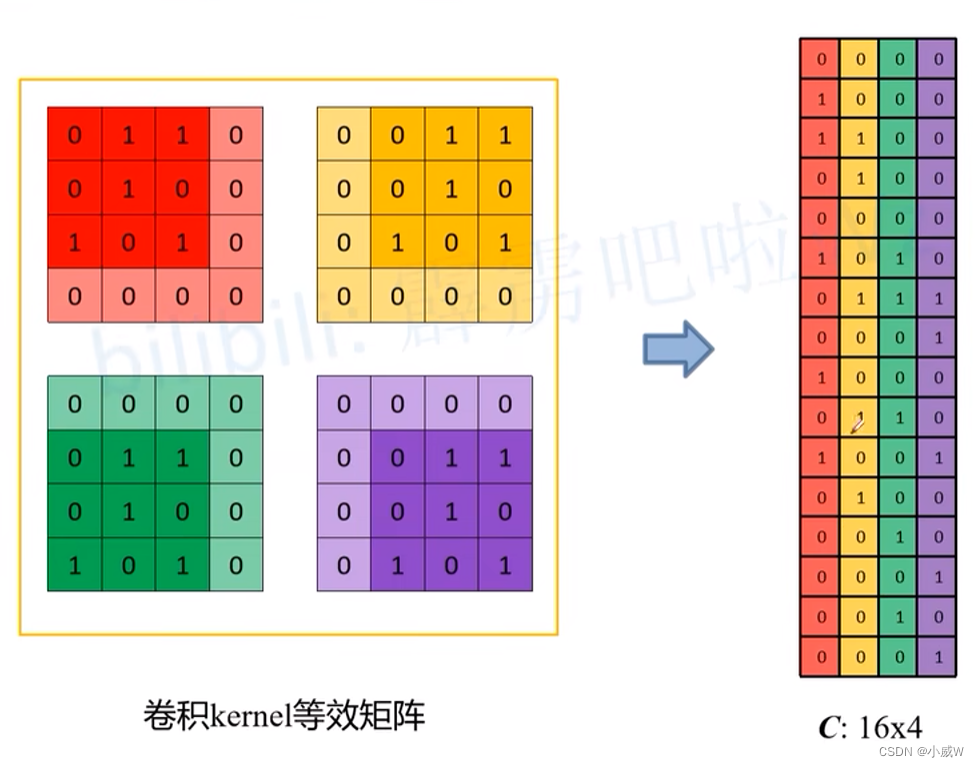
普通卷积 的计算在这里插入图片描述

下面进行另外一种运算，将卷积核 构造 等效矩阵（即空余位置补0）
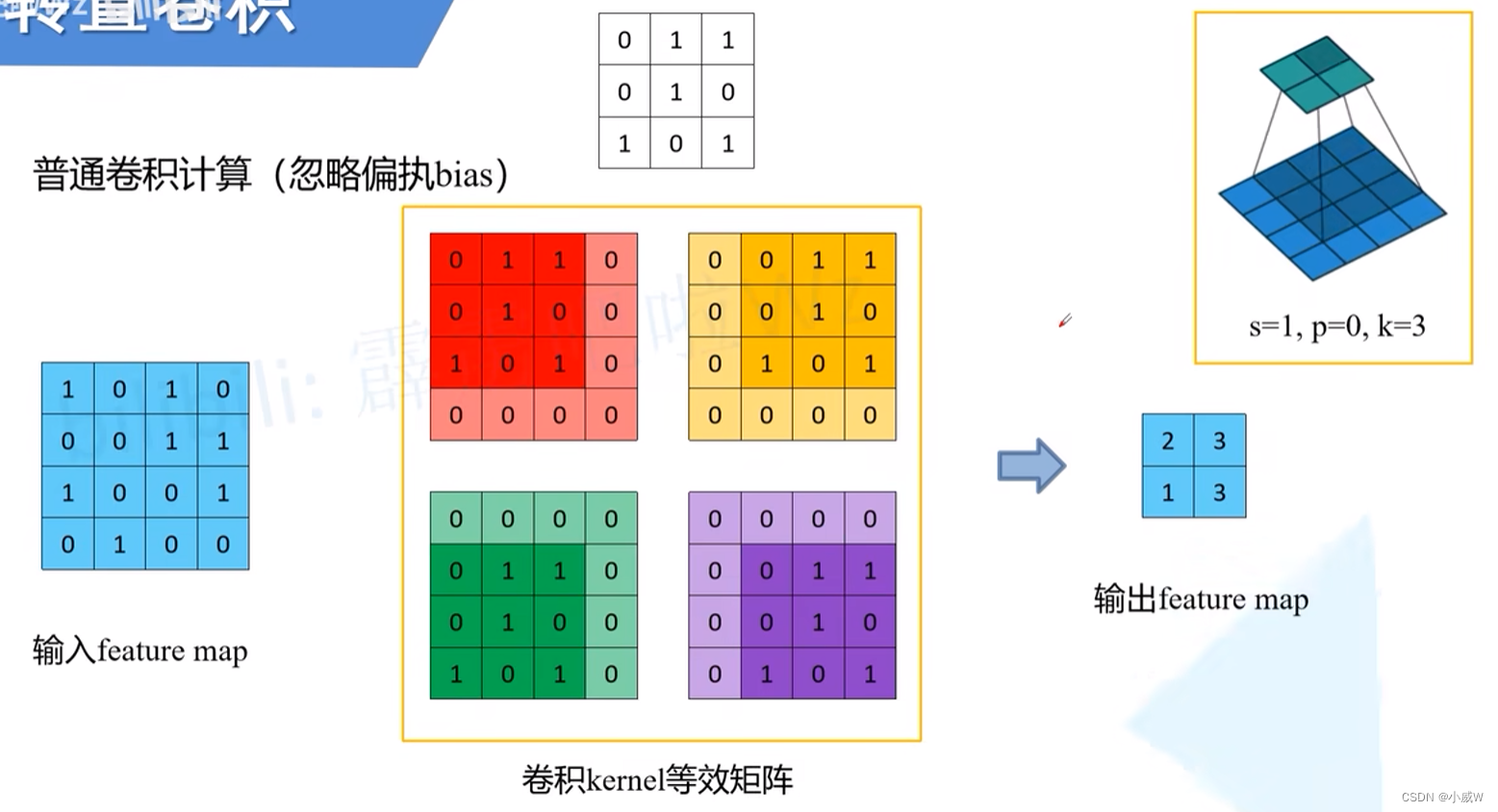
在这里插入图片描述

将 feature map 展平
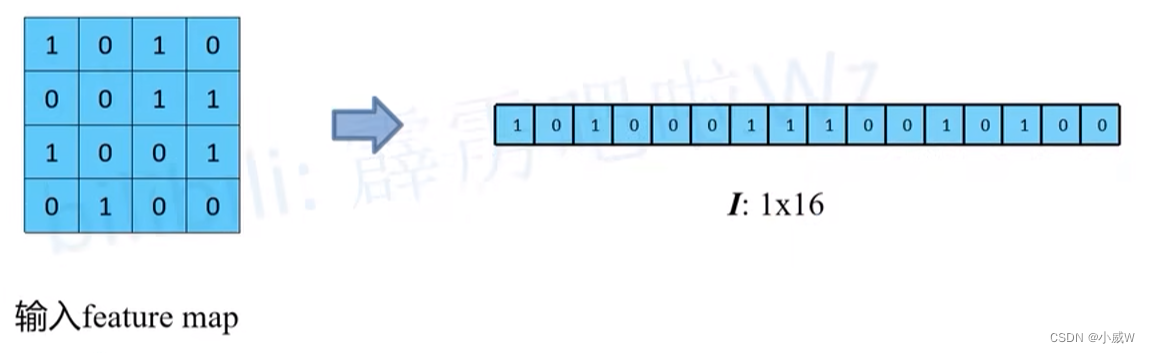
在这里插入图片描述
将 kernel等效矩阵 展平后合并
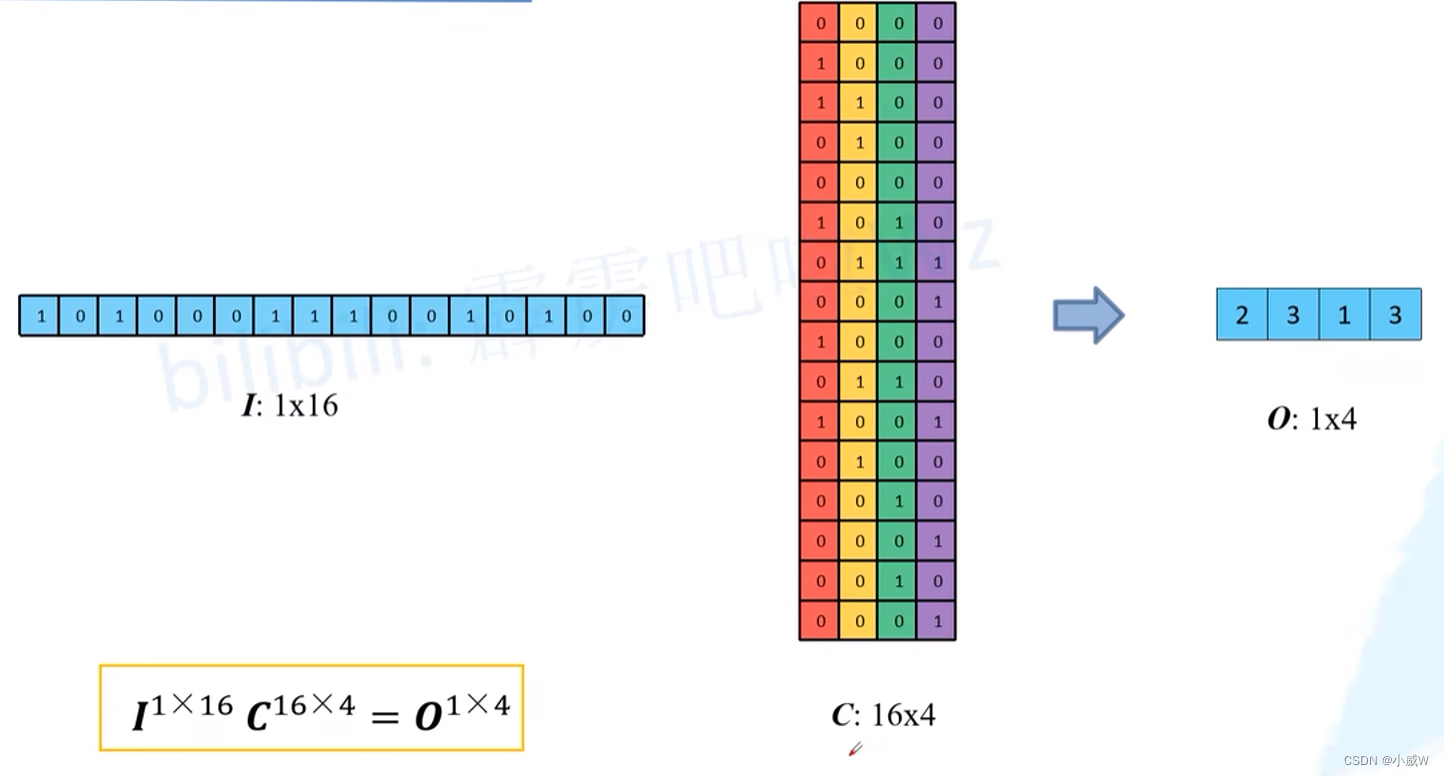
在这里插入图片描述

将I矩阵和C矩阵进行矩阵相乘计算，得到 1 × 4大小的输出。
在这里插入图片描述

==》从C 和 O 不能得到 I，因为C不一定有逆矩阵。但是C有转置矩阵，可以令O与C的转置相乘。

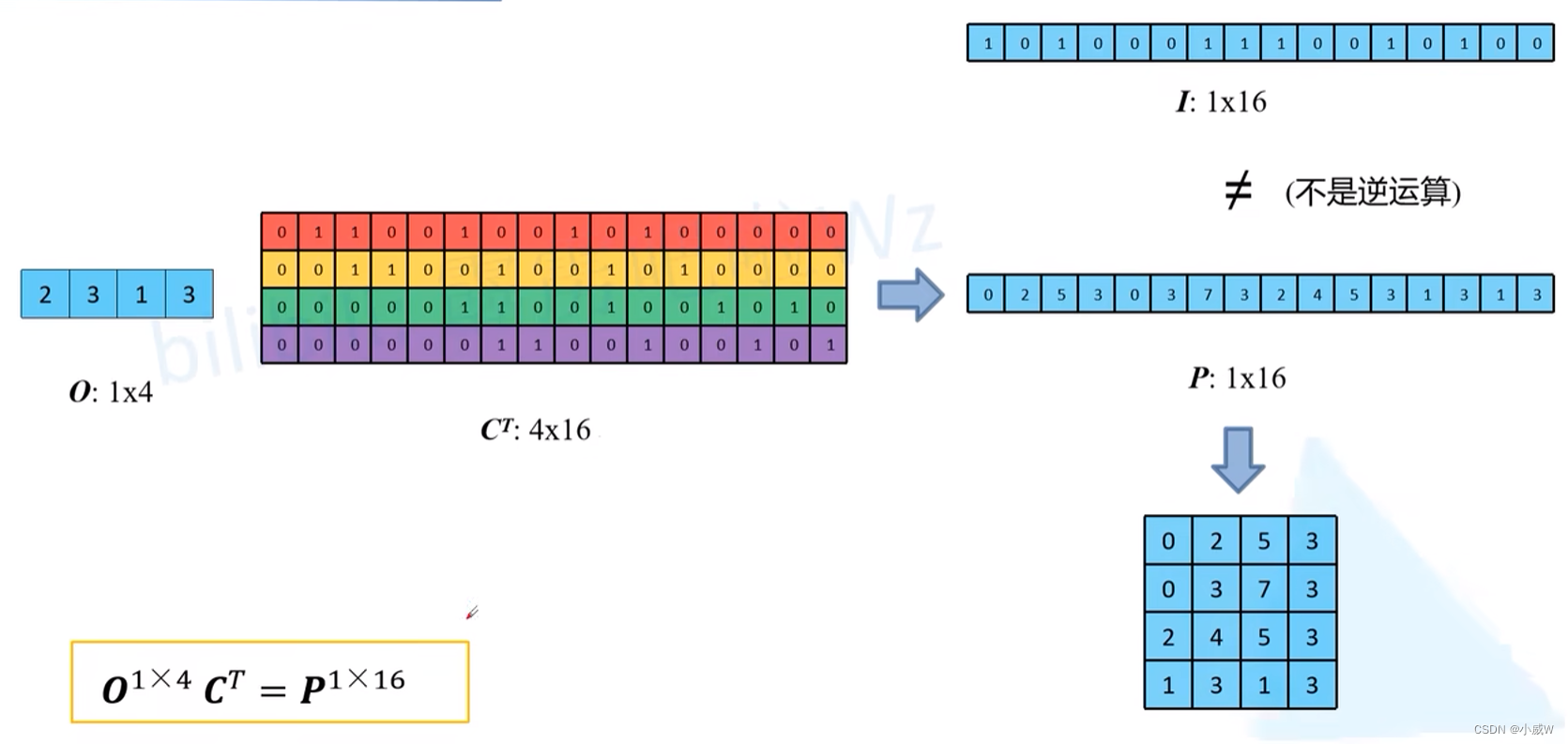
在这里插入图片描述
可以发现得到的结果reshape后就是转置卷积计算的结果，这就是转置卷积的计算过程。

一个神奇的现象，将C的转置按列分来后reshap，可以得到16个小矩阵。

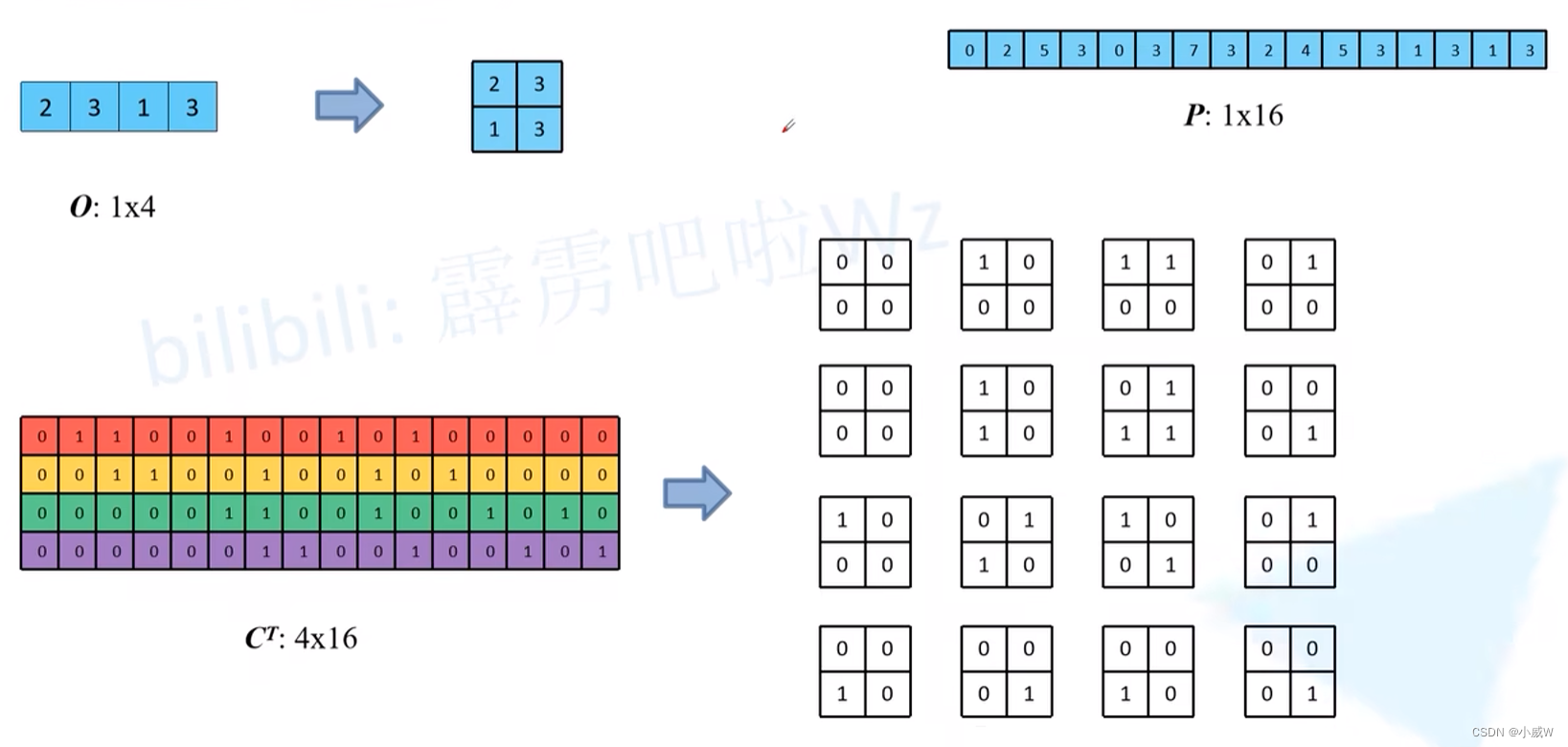
在这里插入图片描述

这16个小卷积分别和普通卷积输出进行卷积计算的结果，就是转置卷积的结果！

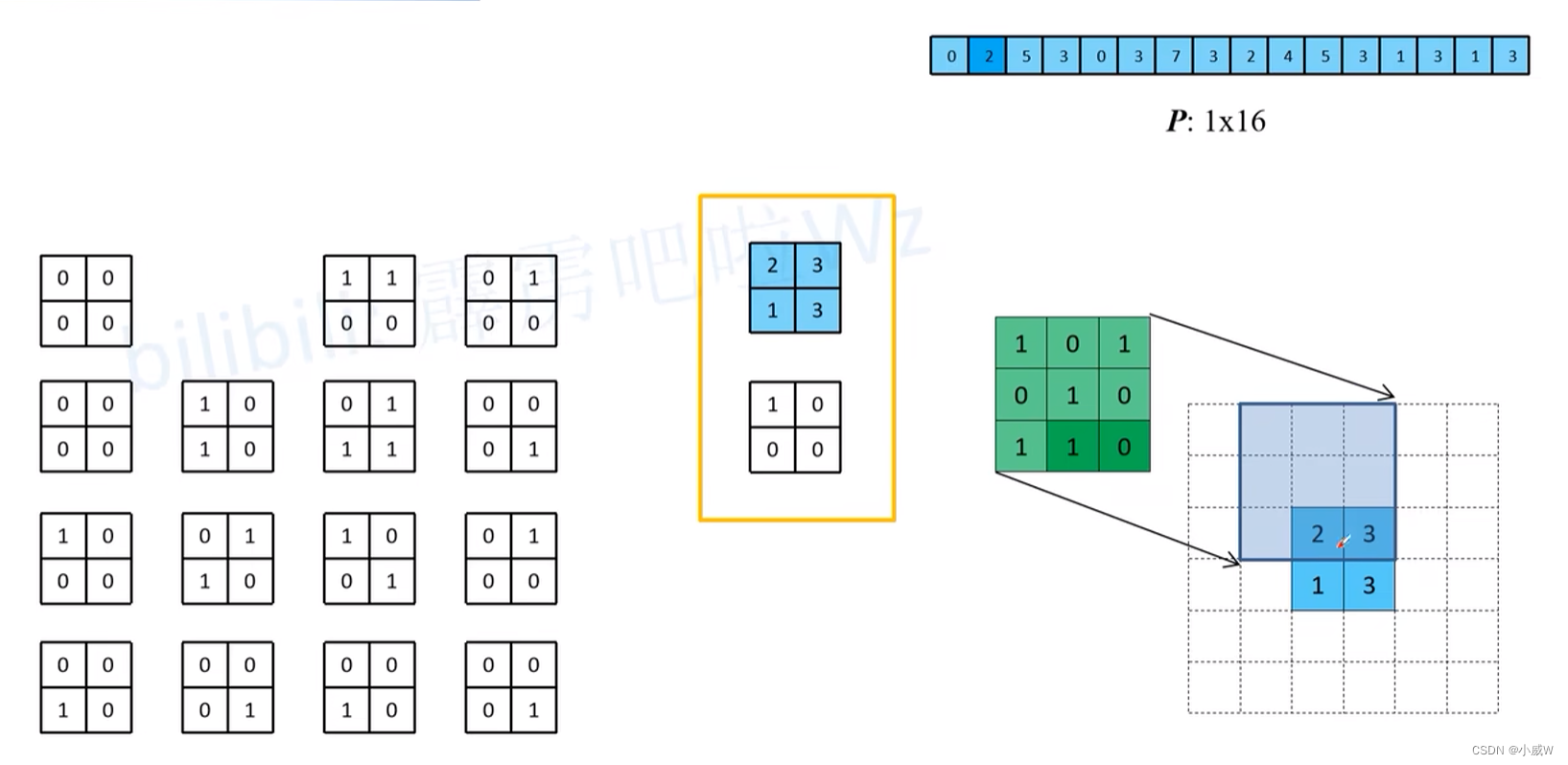
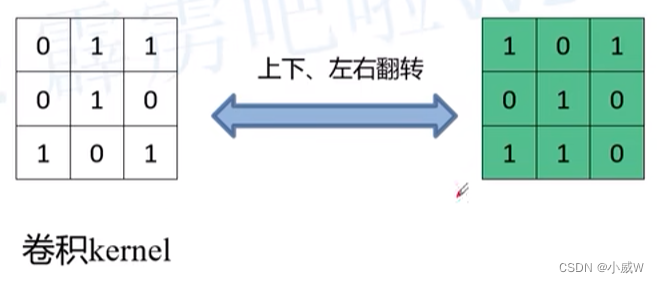
在这里插入图片描述
在这里插入图片描述

参考资料：
https://blog.csdn.net/qq_37541097/article/details/120709865
https://www.bilibili.com/video/BV1mh411J7U4/?vd_source=25159b705a7bd142ef4cf6ae83653ad3

词库加载错误:未能找到文件“E:\highferrum_mysql\Configuration\Dict_Stopwords.txt”。

上一篇：为什么一定要多来几次山西？这篇指南告诉你！

下一篇：ssh： connect to host localhost port 22: Connection refused解决方法

相关内容

热门资讯

Linux指令之搜索查找类 文章目录前言一、搜索查找类find指令locate指令grep指令和管道符号| 前言 上一篇我们学...
English Learnin... English Learning - L2 第 7 次小组纠音 辅音 [p] [b] [t] [d]...
Opencv+Python学习... 一，色彩空间分类1.GRAY色彩空间GRAY（灰度图像）通...
【SSM】MyBatis(三.... 文章目录1.environment2.transactionManager3. dataSource...
甘南七日全景精华游攻略：预算拆... 甘南，这片被《孤独星球》评为“亚洲最佳旅行地”的秘境，集藏地信仰、高原风光、草原牧歌于一体。2025...
Cursor太强了，从零开始写... Cursor太强了，从零开始写ChatGLM大模型的微调代码初次体验对话实录问...
LeetCode题解 19(7... 文章目录子集(78)代码解答目标和(494)代码解答 子集(78) 这道题要求我们返回指定数组的所...
在家也能做！广东叉烧包的美味秘... 在广东点心那琳琅满目的世界里，叉烧包宛如一颗熠熠生辉的甜蜜明珠，以其松软绵密的包子皮和香甜多汁的叉烧...
嬴氏酒以「文化传承」为核心，酱... 嬴氏酒以差异化高品质酱香白酒突围，融合中华文化精髓与古法工艺，精准定位、适配商业模型、把握市场痛点，...
江西小炒烟火气秘诀！爆炒 3 ... 在江西的街头巷尾，总能看到这样的场景：简易的灶台支在店门口，猛火灶呼呼作响，厨师手持铁锅上下翻飞，油...
原创 从... 5月29日，台湾旺旺集团总经理蔡旺庭的发言，直接把人整破防了！他坦诚，旺旺从中国台湾起步，在大陆这片...
从“吸引年轻人”到“成为年轻人... 据后浪研究所发布的《2024年年轻人喝酒报告》显示，00后最爱的网红酒里，汾酒作为唯一上榜的白酒品牌...
亚朵酒店养生早餐获好评，以中式... 近年来，随着健康理念的普及与生活节奏的加快，早餐这一日常场景被重新置于大众视野。而在差旅频繁的客群中...
【XKA六周年特别企划】品牌背... 在大健康的赛道上，愿与XKA合作，开发更多更好的主粮产品，守护家人健康。 2019年通过展会结识XK...
原创 人... 从餐厅搬到火车车厢，自助餐的“边界”正在不断延伸。 据多家媒体报道，近日，从沈阳、大连、长春等地...
黄酒文化发源地：一坛酒，千年香 提起中国酒文化，很多人会立刻想到浓香四溢的白酒，或风情万种的葡萄酒，但却容易忽略了黄酒，这种承载着中...
pikachu——xss 反射性（get）都提示get了，肯定跟url栏有关拿到题目...
传统为体，现代为用：劲牌以古法... 长江吐故纳新，不断拥抱新生，才能涤荡初心，砥砺前行，最终拥抱大海。 “长江第一湾”所在的宜宾美酒也一...
红浪翻滚舌尖舞：口味虾的火辣江... 在湘菜的璀璨版图中，口味虾犹如一簇跃动的红色火焰，以其浓烈奔放的香辣滋味，点燃了无数食客的味蕾。这道...
酒厂老板快看！禁酒令下，中小酒... 嘿，各位酒友、酿酒的小伙伴们，我是酒皇叔王杰老师。最近这禁酒令一出，可把不少中小型酒厂、酒坊的老板们...