电机仿真记录(1)-clark、park坐标变换
创始人
2025-05-29 01:02:04
0次
实验平台：matlab2020b
不讲原理，只记录仿真
Clark
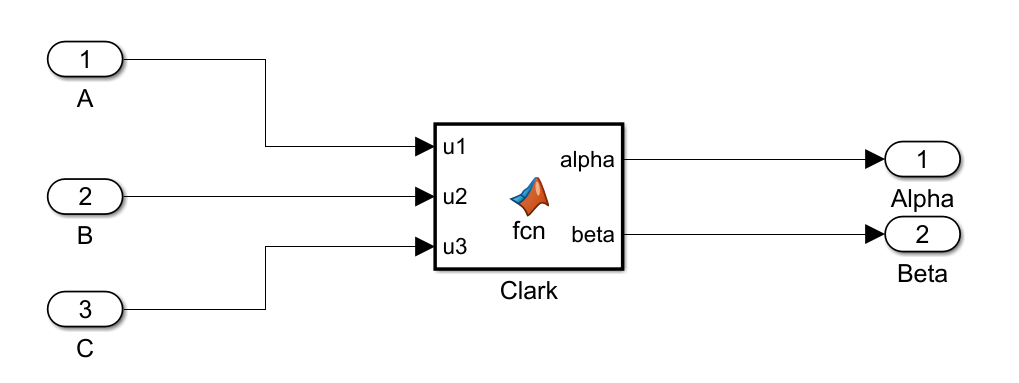
注意，2020之后的版本，都是自己定义函数都是使用的这个模块
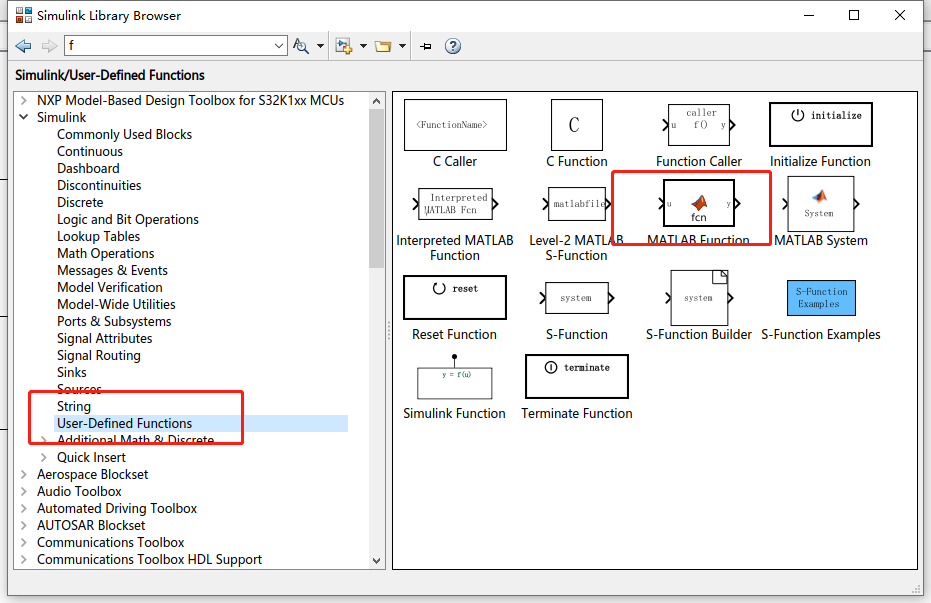
非常的方便把你想输入的公式输进去就可以
function [alpha,beta] = fcn(u1,u2,u3)alpha = (u1-0.5*u2-0.5*u3)*2/3;
beta = (sqrt(3)/2*u2-sqrt(3)/2*u3)*2/3;三个正弦波注意别忘了120°的相位差！
仿真结果：
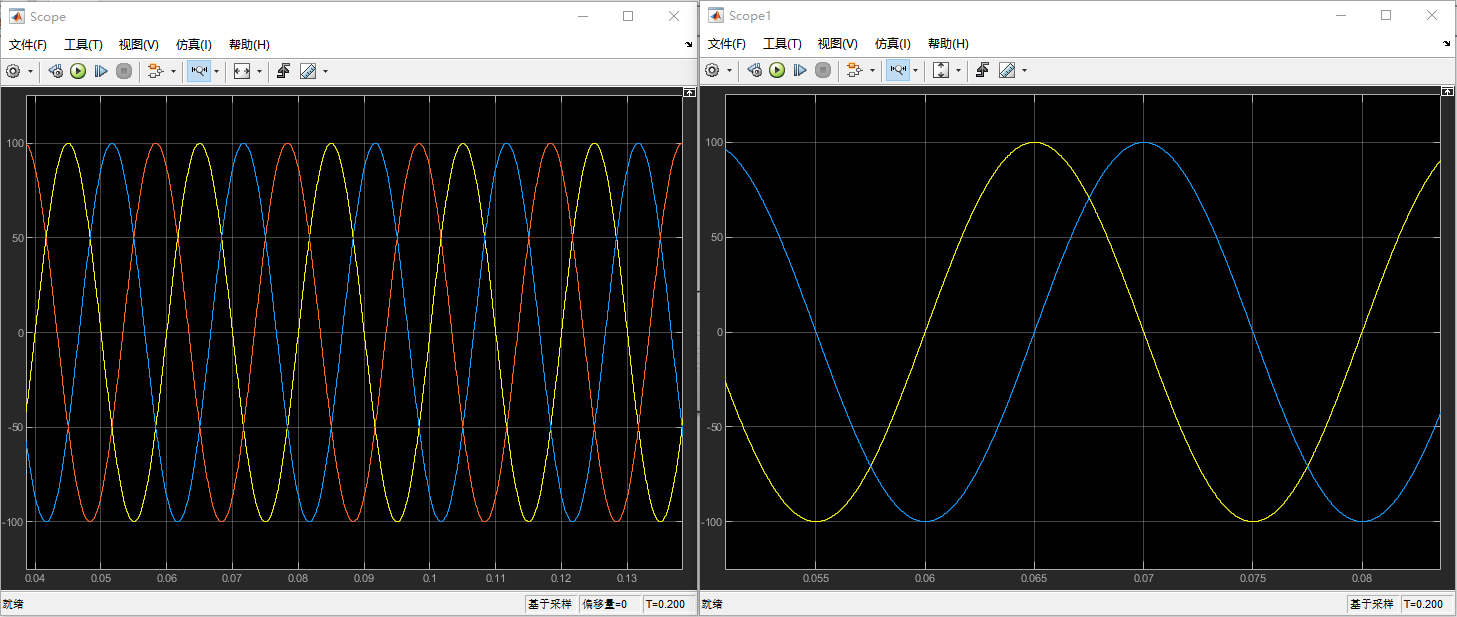
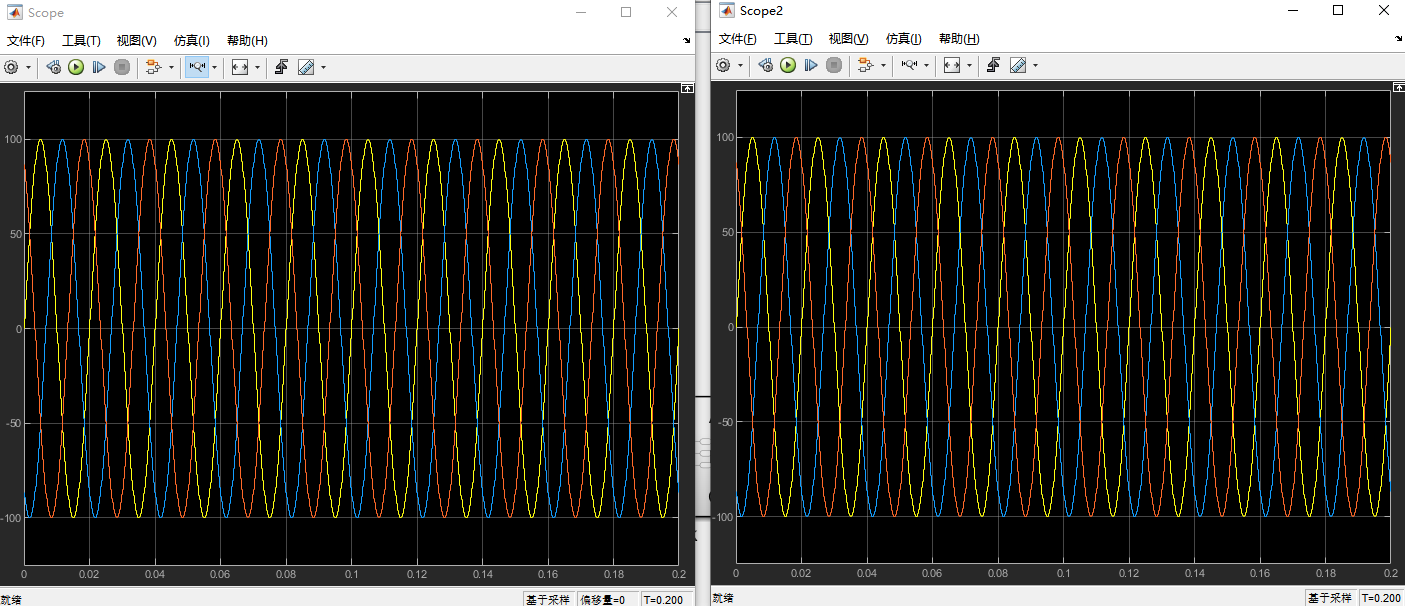
成功！！！！输出的alpha与beta相差90°，且幅值相同！
Clark反变换也是一样的，公式如下
function [u1,u2,u3] = fcn(alpha,beta)u1 = alpha;
u2 = -0.5*alpha + sqrt(3)/2*beta;
u3 = -0.5*alpha - sqrt(3)/2*beta;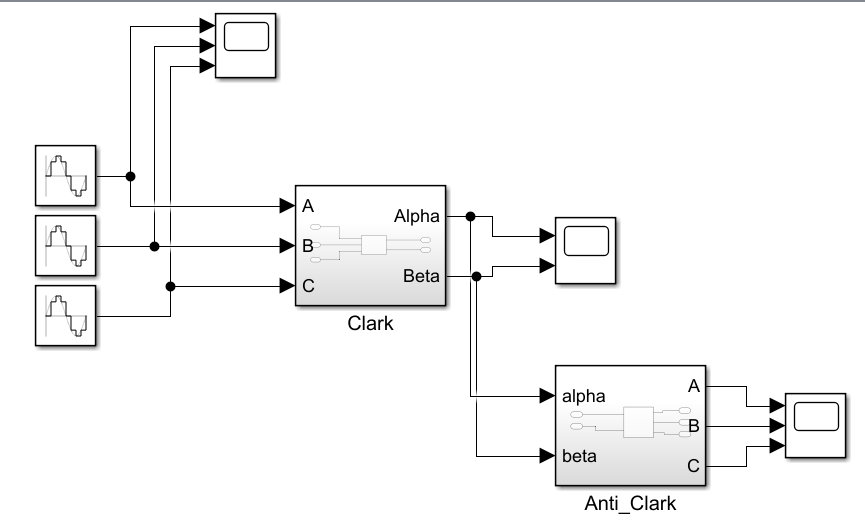
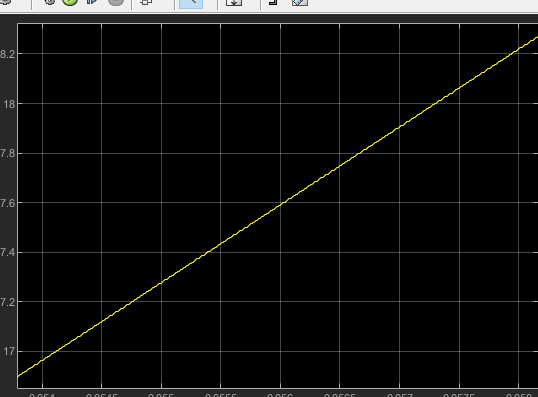
示波器显示：经过clark变换与反变换之后，波形完全相同
Park
公式：
function [d,q] = fcn(u1,u2,u3)d = u1*cos(u3) + u2*sin(u3);
q = -u1*sin(u3) + u2*cos(u3);建模：
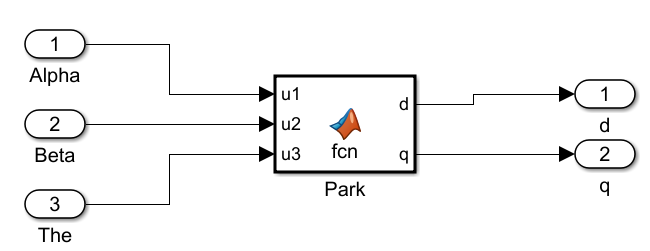
会发现怎么还有一个3 The，这个是d轴与两相静止坐标系α轴的夹角。
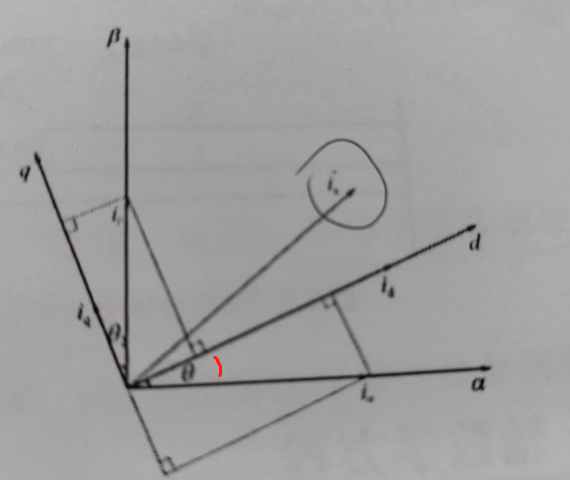
输入的α与β正弦波别忘了90°的相位差。
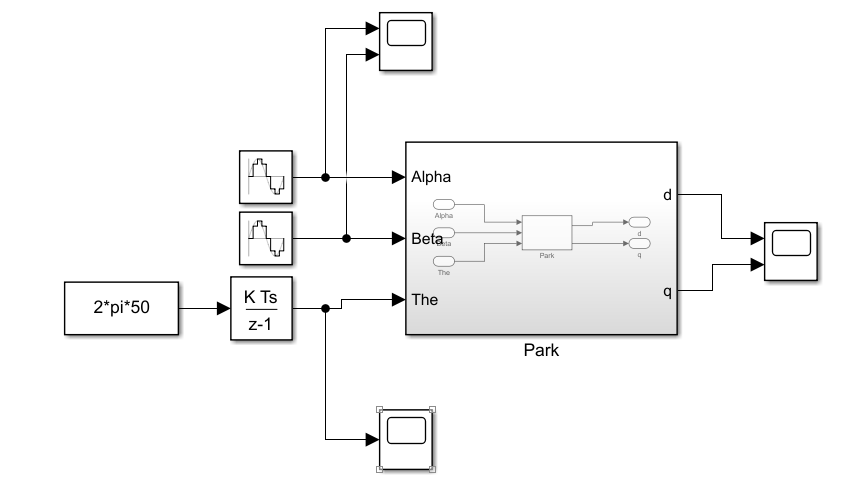
另外θ是一个一直在变化的值，离散非连续，所以咱们用Discrete-Time Integrator模块，让它像梯子一样，跳变~
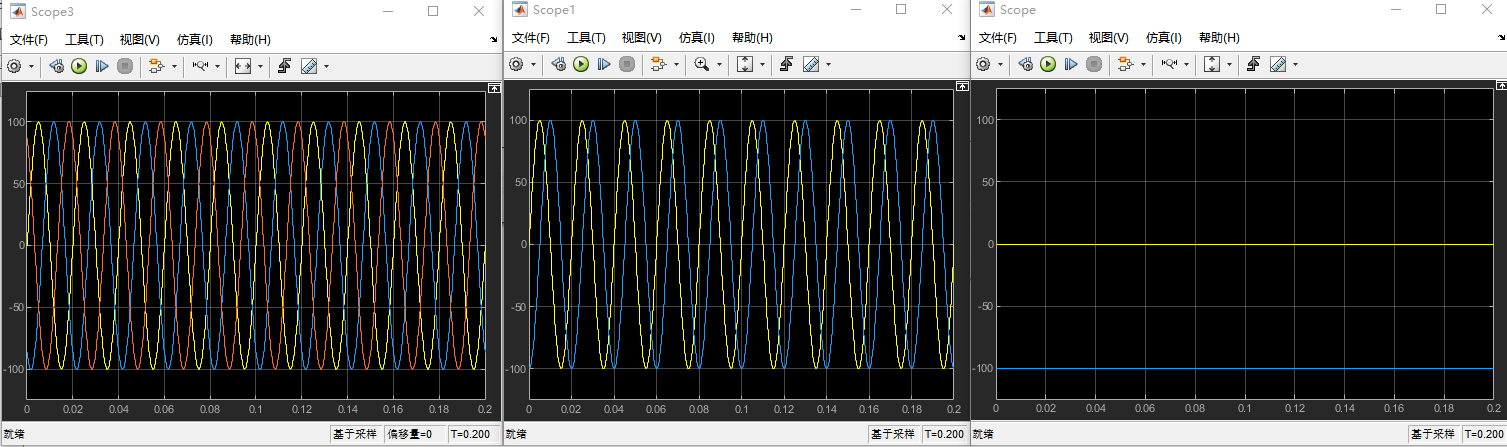
咱们尝试把Clark与park放在一起！
相关内容
热门资讯
节假日胖东来吸引大量外地游客，...
极目新闻记者 詹钘 端午假期，河南许昌胖东来持续火爆，吸引了大量外地游客。6月1日，有许昌当地出租车...
乡村舞台变身奇幻乐园，“童梦奇...
6月1日，“童梦奇缘 乐在桦墅”金陵艺术村落六一主题活动，在栖霞区桦墅村如约启幕。这座掩映在青山绿水...
刚刚！上海警方通报迪士尼打架事...
据@警民直通车-浦东 通报：5月31日18时许，浦东公安分局接报警称迪士尼乐园内有人打架。经初步调查...
3600亿打造最难修的铁路，川...
随着5月21日拉萨-林芝铁路扩能改造项目的招标公告发布，川藏铁路的建设步伐愈加加速。乍一看，这似乎是...
【MySQL】锁
锁 文章目录锁全局锁表级锁表锁元数据锁（MDL）意向锁AUTO-INC锁...
Centos7安装升级最新版R...
Centos7安装升级最新版Redis7.0.10 闭坑攻略1、前言2、升级GCC3、下载编译Red...
2023年长租公寓行业研究报告
第一章 行业概况 长租公寓是一种新型的住房形式，它为租客提供长期的住宿选择...
《全国儿童友好公园打卡地图》在...
中新网广州6月1日电 (记者 程景伟)广州市儿童公园6月1日开启2025年“童迎十五运活力向未来”六...
终于弄明白6-7月去威海，怎么...
威海攻略做好了！去威海不下5次了，建议还没去的姐妹看完这篇再出发，不然真的会不小心就踩雷，去威海玩的...
宜昌三峡三天两晚品质旅游行程，...
宜昌三峡，那是一幅流动的山水画卷，自古以来就吸引着无数文人墨客和游客。这里既有壮美的自然风光，又有深...
做一个元气满满的同路人，在社科...
人生需要归零。每过一段时间都要将过去清零，让自己重新开始。该放手时就放手，...
微软WHQL认证有哪些步骤？驱...
微软WHQL认证是指Microsoft Windows Hardware Quality Labs&...
移动应用架构设计：如何转变开发...
移动应用架构设计：如何转变开发流程 2023 年掌握移动应用程序架构的指南...
原创 最...
夏天开个火炒个菜，汗珠子噼里啪啦往下掉，油烟一熏，胃口都跑没影儿了。这时候，谁还乐意在灶台边吭哧吭哧...
蔬菜中的“维 C 之王”竟是它...
在蔬菜界中，甜椒以其鲜艳的色彩和清脆的口感，常常被当作菜肴的点缀。无论是青红黄相间的炒菜，还是沙拉中...
翠湖又添打卡地！这幅墙绘让三角...
端午假期，春城市民不用出远门也能邂逅众多风景。在翠湖边，“一名”簪花少女悄然现身，吸引了众多市民游客...
当端午遇上“六一” 两江新区景...
三大动漫IP集结、 萌趣恐龙巡游、泰式泼水狂欢..... 6月1日， 端午假期邂逅“六一”儿童节， ...
夏日文旅新地标 来璧山梦界水世...
6月1日，璧山梦界水世界在玉泉湖畔开园。开园首日即迎来众多游客，共同见证了一场融合“水战”激情、亲子...